第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025河南南阳月考」计算$(2m+1)(3m-2)$,结果正确的是(
A.$6m^{2}-m-2$
B.$6m^{2}+m-2$
C.$6m^{2}-2$
D.$5m-1$
A
)A.$6m^{2}-m-2$
B.$6m^{2}+m-2$
C.$6m^{2}-2$
D.$5m-1$
答案:
A $(2m + 1)(3m - 2) = 2m\cdot3m - 2m\times2 + 3m\times1 - 1\times2 = 6m^{2} - m - 2$,故选A.
2.如图,下列整式中不能正确表示图中阴影部分的面积的是(
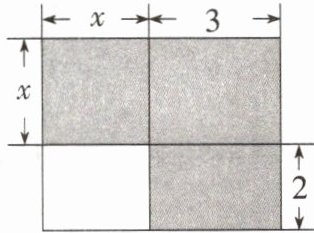
A.$x^{2}+3(x+2)$
B.$x(x+3)+6$
C.$x(x+3)+2(x+3)$
D.$(x+3)(x+2)-2x$
C
)
A.$x^{2}+3(x+2)$
B.$x(x+3)+6$
C.$x(x+3)+2(x+3)$
D.$(x+3)(x+2)-2x$
答案:
C 题图中阴影部分的面积为$x^{2} + 3(x + 2)$或$x(x + 3) + 6$或$(x + 3)(x + 2) - 2x$,故选C.
3.「2025湖南师大附中期末」设$M= (x-3)(x-4)$,$N= (x-2)(x-5)$,则M与N的关系为(
A.$M>N$
B.$M<N$
C.$M= N$
D.无法确定
A
)A.$M>N$
B.$M<N$
C.$M= N$
D.无法确定
答案:
A $\because M = (x - 3)(x - 4) = x^{2} - 7x + 12$,$N = (x - 2)(x - 5) = x^{2} - 7x + 10$,$\therefore M - N = x^{2} - 7x + 12 - (x^{2} - 7x + 10) = 2 > 0$,$\therefore M > N$. 故选A.
4.「2025湖南衡阳期中」若$(2x+m)(x-3)$展开后的结果不含x的一次项,则m的值是____
6
.
答案:
答案 6
解析 $(2x + m)(x - 3) = 2x^{2} - 6x + mx - 3m$,$\because (2x + m)\cdot(x - 3)$展开后的结果不含$x$的一次项,$\therefore - 6x + mx = (m - 6)x = 0$,$\therefore m = 6$. 故答案为6.
解析 $(2x + m)(x - 3) = 2x^{2} - 6x + mx - 3m$,$\because (2x + m)\cdot(x - 3)$展开后的结果不含$x$的一次项,$\therefore - 6x + mx = (m - 6)x = 0$,$\therefore m = 6$. 故答案为6.
5.若$2x^{3}-ax^{2}-5x+5= (2x^{2}+ax-1)(x-b)+3$,其中a,b为整数,则$a+b$的值为____
4
.
答案:
答案 4
解析 $\because 2x^{3} - ax^{2} - 5x + 5 = (2x^{2} + ax - 1)(x - b) + 3$,
$\therefore 2x^{3} - ax^{2} - 5x + 5 = 2x^{3} + (a - 2b)x^{2} - (ab + 1)x + b + 3$,
$\therefore a - 2b = - a$,$-(ab + 1) = - 5$,$b + 3 = 5$,
解得$b = 2$,$a = 2$,$\therefore a + b = 2 + 2 = 4$.
解析 $\because 2x^{3} - ax^{2} - 5x + 5 = (2x^{2} + ax - 1)(x - b) + 3$,
$\therefore 2x^{3} - ax^{2} - 5x + 5 = 2x^{3} + (a - 2b)x^{2} - (ab + 1)x + b + 3$,
$\therefore a - 2b = - a$,$-(ab + 1) = - 5$,$b + 3 = 5$,
解得$b = 2$,$a = 2$,$\therefore a + b = 2 + 2 = 4$.
6.计算:
(1)$(2a+b)(a-2b)+2a(b-a)$.
(2)$2x(x-4)-(2x-3)(x+2)$.
(1)$(2a+b)(a-2b)+2a(b-a)$.
(2)$2x(x-4)-(2x-3)(x+2)$.
答案:
解析
(1)$(2a + b)(a - 2b) + 2a(b - a)$
$= 2a^{2} - 4ab + ab - 2b^{2} + 2ab - 2a^{2} = - ab - 2b^{2}$.
(2)$2x(x - 4) - (2x - 3)(x + 2)$
$= 2x^{2} - 8x - (2x^{2} - 3x + 4x - 6)$
$= 2x^{2} - 8x - 2x^{2} + 3x - 4x + 6 = - 9x + 6$.
(1)$(2a + b)(a - 2b) + 2a(b - a)$
$= 2a^{2} - 4ab + ab - 2b^{2} + 2ab - 2a^{2} = - ab - 2b^{2}$.
(2)$2x(x - 4) - (2x - 3)(x + 2)$
$= 2x^{2} - 8x - (2x^{2} - 3x + 4x - 6)$
$= 2x^{2} - 8x - 2x^{2} + 3x - 4x + 6 = - 9x + 6$.
7.先化简,再求值:$2x(x-1)+(x-2)(x+7)$,其中$x= -4$.
答案:
解析 原式$= 2x^{2} - 2x + x^{2} + 7x - 2x - 14 = 3x^{2} + 3x - 14$.
当$x = - 4$时,原式$= 3\times(- 4)^{2} + 3\times(- 4) - 14 = 22$.
当$x = - 4$时,原式$= 3\times(- 4)^{2} + 3\times(- 4) - 14 = 22$.
8.「2025云南大理州期末」如图,某小区有一块长为$(3a+2b)$米,宽为$(2a-3b)$米的长方形地块,角上有四个边长为b米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)求该小区绿化的总面积.
答:该小区绿化的总面积为
(2)若$a= 10$,$b= 2$,绿化成本为50元/平方米,则完成绿化共需要多少钱?
答:完成绿化共需要
(1)求该小区绿化的总面积.
答:该小区绿化的总面积为
$(6a^{2} - 5ab - 10b^{2})$
平方米.(2)若$a= 10$,$b= 2$,绿化成本为50元/平方米,则完成绿化共需要多少钱?
答:完成绿化共需要
23000
元.
答案:
解析
(1)$(3a + 2b)(2a - 3b) - 4b^{2}$
$= 6a^{2} + 4ab - 9ab - 6b^{2} - 4b^{2}$
$= 6a^{2} - 5ab - 10b^{2}$.
答:该小区绿化的总面积为$(6a^{2} - 5ab - 10b^{2})$平方米.
(2)当$a = 10$,$b = 2$时,
$6a^{2} - 5ab - 10b^{2} = 6\times10^{2} - 5\times10\times2 - 10\times2^{2} = 460$,
$50\times460 = 23000$(元).
答:完成绿化共需要23000元.
(1)$(3a + 2b)(2a - 3b) - 4b^{2}$
$= 6a^{2} + 4ab - 9ab - 6b^{2} - 4b^{2}$
$= 6a^{2} - 5ab - 10b^{2}$.
答:该小区绿化的总面积为$(6a^{2} - 5ab - 10b^{2})$平方米.
(2)当$a = 10$,$b = 2$时,
$6a^{2} - 5ab - 10b^{2} = 6\times10^{2} - 5\times10\times2 - 10\times2^{2} = 460$,
$50\times460 = 23000$(元).
答:完成绿化共需要23000元.
9.「2025湖南长沙期末」若$(y+2)(y-3)= y^{2}+my+n$,则m,n的值分别为(
A.$-1$,$-6$
B.$1$,$-6$
C.$1$,$6$
D.$5$,$-6$
A
)A.$-1$,$-6$
B.$1$,$-6$
C.$1$,$6$
D.$5$,$-6$
答案:
A $\because (y + 2)(y - 3) = y^{2} - y - 6 = y^{2} + my + n$,$\therefore m = - 1$,$n = - 6$. 故选A.
10.「2025海南儋州期中」若$(x-1)(x+6)= x^{2}+px+q$,则$p+q$的值为(
A.$11$
B.$-11$
C.$-1$
D.$1$
C
)A.$11$
B.$-11$
C.$-1$
D.$1$
答案:
C $\because (x - 1)(x + 6) = x^{2} + 5x - 6 = x^{2} + px + q$,$\therefore p = 5$,$q = - 6$,$\therefore p + q = - 1$,故选C.
11.「2025福建福州期末,★☆」已知a,b是常数,若化简$(x-a)(2x^{2}+bx-4)$的结果不含x的二次项,则$12a-6b-1$的值为(
A.$1$
B.$-1$
C.$5$
D.$-13$
B
)A.$1$
B.$-1$
C.$5$
D.$-13$
答案:
B $(x - a)(2x^{2} + bx - 4) = 2x^{3} + (- 2a + b)x^{2} + (- ab - 4)x + 4a$,$\because$化简$(x - a)(2x^{2} + bx - 4)$的结果不含$x$的二次项,$\therefore - 2a + b = 0$,$\therefore b = 2a$,$\therefore 12a - 6b - 1 = 12a - 6\times2a - 1 = - 1$. 故选B.
查看更多完整答案,请扫码查看


