《2025年5年中考3年模拟八年级数学上册人教版》

10. 新课标 中华优秀传统文化 [2025 河南漯河期中,★☆] 为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间,图 1 是某同学“抖空竹”时的一个瞬间,小聪把它抽象成图 2,已知$AB // CD$,$∠EAB = 80^{\circ}$,$∠ECD = 110^{\circ}$,则$∠E$的度数是(

)
A. $30^{\circ}$
B. $35^{\circ}$
C. $40^{\circ}$
D. $45^{\circ}$

答案：
A 如图，

延长DC交AE于点F，
∵AB // CD，
∴∠EFC = ∠EAB = 80°，
∵∠ECD是△ECF的一个外角，
∴∠E = ∠ECD - ∠EFC = 110° - 80° = 30°. 故选 A.

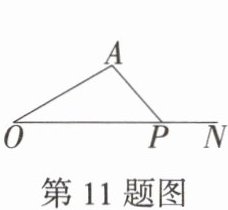
11. [2025 江西南昌期中,★☆] 如图,已知点$P是射线ON$上一动点(不与点$O$重合),$∠O = 30^{\circ}$,若$△AOP$为钝角三角形,则$∠A$的取值范围是(D)

A. $0^{\circ} ＜ ∠A ＜ 60^{\circ}$
B. $90^{\circ} ＜ ∠A ＜ 180^{\circ}$
C. $0^{\circ} ＜ ∠A ＜ 30^{\circ}或90^{\circ} ＜ ∠A ＜ 130^{\circ}$
D. $0^{\circ} ＜ ∠A ＜ 60^{\circ}或90^{\circ} ＜ ∠A ＜ 150^{\circ}$

答案： D 若∠A为钝角，则90° ＜ ∠A ＜ 180° - 30°，即90° ＜ ∠A ＜ 150°，若∠A为锐角，则0° ＜ ∠APN ＜ 90°，
∵∠APN = ∠O + ∠A，
∴∠A + 30° ＜ 90°，
∴0° ＜ ∠A ＜ 60°. 综上，∠A的取值范围为0° ＜ ∠A ＜ 60°或90° ＜ ∠A ＜ 150°. 故选 D.

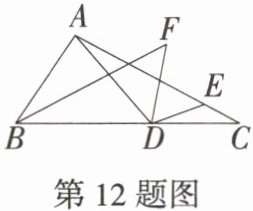
12. [2025 江苏泰州月考,★☆] 如图,$△ABC$中,$∠ABC = 3∠C$,点$D$,$E分别在边BC$,$AC$上,$∠EDC = 20^{\circ}$,$∠ADE = 3∠AED$,$∠ABC的平分线与∠ADE的平分线交于点F$,则$∠F$的度数是(A)

A. $50^{\circ}$
B. $55^{\circ}$
C. $60^{\circ}$
D. $65^{\circ}$

答案： A
∵BF平分∠ABC，
∴∠FBC = $\frac{1}{2}$∠ABC，
∵∠ABC = 3∠C，
∴∠FBC = $\frac{3}{2}$∠C，设∠C = x，则∠FBC = $\frac{3}{2}$x，
∵∠EDC = 20°，
∴∠AED = ∠C + ∠EDC = x + 20°，
∵∠ADE = 3∠AED，
∴∠ADE = 3x + 60°，
∵DF平分∠ADE，
∴∠EDF = $\frac{3}{2}$x + 30°，
∵∠FDC = ∠F + ∠FBC，
∴$\frac{3}{2}$x + 30° + 20° = ∠F + $\frac{3}{2}$x，
∴∠F = 50°. 故选 A.

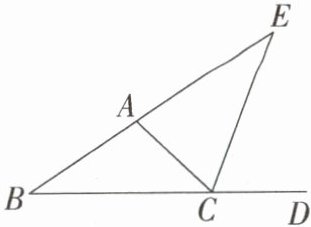
13. [★☆] 如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)求证：∠BAC = ∠B + 2∠E.
(2)若∠B = 30°,∠ACB = 40°,求∠E的度数.

(1)证明：∵CE平分∠ACD，∴∠ECD = ∠ACE. ∵∠BAC = ∠E + ∠ACE，∴∠BAC = ∠E + ∠ECD，∵∠ECD = ∠B + ∠E，∴∠BAC = ∠E + ∠B + ∠E，∴∠BAC = ∠B + 2∠E.
(2)40°

答案： 解析
(1) 证明：
∵CE平分∠ACD，
∴∠ECD = ∠ACE.
∵∠BAC = ∠E + ∠ACE，
∴∠BAC = ∠E + ∠ECD，
∵∠ECD = ∠B + ∠E，
∴∠BAC = ∠E + ∠B + ∠E，
∴∠BAC = ∠B + 2∠E.
(2)
∵CE平分∠ACD，
∴∠ACE = ∠ECD，
∵∠ACB = 40°，
∴∠ECD = $\frac{1}{2}$×(180° - 40°) = 70°，
∴∠E = ∠ECD - ∠B = 70° - 30° = 40°.

14. 新课标 推理能力 [2024 河南南阳期末] 【概念认识】
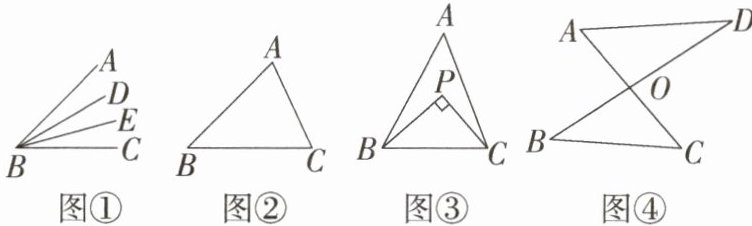
如图①,在$∠ABC$中,若$∠ABD = ∠DBE = ∠EBC$,则$BD$,$BE叫作∠ABC$的“三分线”,其中,$BD$是“邻$AB$三分线”,$BE$是“邻$BC$三分线”.
【问题解决】
(1)如图②,在$△ABC$中,$∠A = 70^{\circ}$,$∠B = 45^{\circ}$,若$∠B$的“三分线”$BD交AC于点D$,则$∠BDC$的度数为______.
(2)如图③,在$△ABC$中,$BP和CP分别是∠ABC$的“邻$AB$三分线”和$∠ACB$的“邻$AC$三分线”,且$BP \perp CP$,求$∠A$的度数.
【延伸推广】
(3)如图④,直线$AC$、$BD交于点O$,$∠ADB$的“三分线”所在的直线与$∠ACB$的“三分线”所在的直线交于点$P$.若$∠A = 66^{\circ}$,$∠B = 45^{\circ}$,$∠ADB = m^{\circ}$,直接写出$∠DPC$的度数.

答案：
解析
(1)85°或100°. 详解：如图，

∵∠ABC = 45°，BD，BD'是∠ABC的“三分线”，
∴∠ABD = ∠DBD' = ∠D'BC = $\frac{1}{3}$∠ABC = 15°，
∵∠A = 70°，
∴∠BDC = ∠A + ∠ABD = 70° + 15° = 85°，∠BD'C = ∠A + ∠ABD' = 70° + 15° + 15° = 100°. 故答案为85°或100°.
(2)
∵BP ⊥ CP，
∴∠BPC = 90°，
∴∠PBC + ∠PCB = 90°，
∵BP和CP分别是∠ABC的“邻AB三分线”和∠ACB的“邻AC三分线”，
∴∠PBC = $\frac{2}{3}$∠ABC，∠PCB = $\frac{2}{3}$∠ACB，
∴$\frac{2}{3}$∠ABC + $\frac{2}{3}$∠ACB = 90°，
∴∠ABC + ∠ACB = 135°，
∴∠A = 180° - (∠ABC + ∠ACB) = 180° - 135° = 45°.
(3)59°或52°或(52 - $\frac{1}{3}$m)°或(59 + $\frac{1}{3}$m)°. 详解：分四种情况讨论：
①如图 1，当DP和CP分别是∠ADB的“邻AD三分线”和∠ACB的“邻BC三分线”时，
∠ADE = $\frac{1}{3}$∠ADB = $\frac{1}{3}$m°，∠ACP = $\frac{2}{3}$∠ACB，
∵∠AOD = ∠BOC，
∴∠A + ∠ADB = ∠B + ∠ACB，
∵∠A = 66°，∠B = 45°，∠ADB = m°，
∴66° + m° = 45° + ∠ACB，
∴∠ACB = 21° + m°，
∴∠ACP = $\frac{2}{3}$∠ACB = 14° + $\frac{2}{3}$m°，
∵∠AED = ∠CEP，
∴∠A + ∠ADE = ∠DPC + ∠ACP，
∴66° + $\frac{1}{3}$m° = ∠DPC + 14° + $\frac{2}{3}$m°，
∴∠DPC = (52 - $\frac{1}{3}$m)°.

②如图 2，当DP和CP分别是∠ADB的“邻AD三分线”和∠ACB的“邻AC三分线”时，
∠ADE = $\frac{1}{3}$∠ADB = $\frac{1}{3}$m°，∠ACP = $\frac{1}{3}$∠ACB，
由①知∠ACB = 21° + m°，
∴∠ACP = 7° + $\frac{1}{3}$m°，
同理得66° + $\frac{1}{3}$m° = ∠DPC + 7° + $\frac{1}{3}$m°，
∴∠DPC = 59°.

③如图 3，当DP和CP分别是∠ADB的“邻DB三分线”和∠ACB的“邻BC三分线”时，
∠ADE = $\frac{2}{3}$∠ADB = $\frac{2}{3}$m°，∠ACP = $\frac{2}{3}$∠ACB，
由①知∠ACB = 21° + m°，
∴∠ACP = 14° + $\frac{2}{3}$m°，
同理得66° + $\frac{2}{3}$m° = ∠DPC + 14° + $\frac{2}{3}$m°，
∴∠DPC = 52°.

④如图 4，当DP和CP分别是∠ADB的“邻DB三分线”和∠ACB的“邻AC三分线”时，
∠ADE = $\frac{2}{3}$∠ADB = $\frac{2}{3}$m°，∠ACP = $\frac{1}{3}$∠ACB，
由①知∠ACB = 21° + m°，
∴∠ACP = 7° + $\frac{1}{3}$m°，
同理得66° + $\frac{2}{3}$m° = ∠DPC + 7° + $\frac{1}{3}$m°，
∴∠DPC = (59 + $\frac{1}{3}$m)°.
综上所述，∠DPC的度数为59°或52°或(52 - $\frac{1}{3}$m)°或(59 + $\frac{1}{3}$m)°.