第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
13. (9分)计算:
(1) $ x^{3} y \cdot x^{3} y^{2}-\left(-2 x^{2} y\right)^{3} $.
(2) $ a^{2} \cdot a^{4}+\left(-2 a^{2}\right)^{3}+a^{8} ÷ a^{2} $.
(3) $ \left(-a^{2} b\right)^{3}+\left(2 a^{7} b^{4}+a b\right) ÷ a b $.
(4) 「2025湖北荆州期末」$ (x+2-3 y)(x+2+3 y) $.
(1) $ x^{3} y \cdot x^{3} y^{2}-\left(-2 x^{2} y\right)^{3} $.
(2) $ a^{2} \cdot a^{4}+\left(-2 a^{2}\right)^{3}+a^{8} ÷ a^{2} $.
(3) $ \left(-a^{2} b\right)^{3}+\left(2 a^{7} b^{4}+a b\right) ÷ a b $.
(4) 「2025湖北荆州期末」$ (x+2-3 y)(x+2+3 y) $.
答案:
解析
(1) $ x ^ { 3 } y \cdot x ^ { 3 } y ^ { 2 } - ( - 2 x ^ { 2 } y ) ^ { 3 } = x ^ { 6 } y ^ { 3 } + 8 x ^ { 6 } y ^ { 3 } = 9 x ^ { 6 } y ^ { 3 } $。
(2) $ a ^ { 2 } \cdot a ^ { 4 } + ( - 2 a ^ { 2 } ) ^ { 3 } + a ^ { 8 } \div a ^ { 2 } = a ^ { 6 } + ( - 8 a ^ { 6 } ) + a ^ { 6 } = - 6 a ^ { 6 } $。
(3) $ ( - a ^ { 2 } b ) ^ { 3 } + ( 2 a ^ { 7 } b ^ { 4 } + a b ) \div a b = - a ^ { 6 } b ^ { 3 } + 2 a ^ { 6 } b ^ { 3 } + 1 = a ^ { 6 } b ^ { 3 } + 1 $。
(4) $ ( x + 2 - 3 y ) ( x + 2 + 3 y ) = [ ( x + 2 ) - 3 y ] [ ( x + 2 ) + 3 y ] = ( x + 2 ) ^ { 2 } - ( 3 y ) ^ { 2 } = x ^ { 2 } + 4 x + 4 - 9 y ^ { 2 } $。
(1) $ x ^ { 3 } y \cdot x ^ { 3 } y ^ { 2 } - ( - 2 x ^ { 2 } y ) ^ { 3 } = x ^ { 6 } y ^ { 3 } + 8 x ^ { 6 } y ^ { 3 } = 9 x ^ { 6 } y ^ { 3 } $。
(2) $ a ^ { 2 } \cdot a ^ { 4 } + ( - 2 a ^ { 2 } ) ^ { 3 } + a ^ { 8 } \div a ^ { 2 } = a ^ { 6 } + ( - 8 a ^ { 6 } ) + a ^ { 6 } = - 6 a ^ { 6 } $。
(3) $ ( - a ^ { 2 } b ) ^ { 3 } + ( 2 a ^ { 7 } b ^ { 4 } + a b ) \div a b = - a ^ { 6 } b ^ { 3 } + 2 a ^ { 6 } b ^ { 3 } + 1 = a ^ { 6 } b ^ { 3 } + 1 $。
(4) $ ( x + 2 - 3 y ) ( x + 2 + 3 y ) = [ ( x + 2 ) - 3 y ] [ ( x + 2 ) + 3 y ] = ( x + 2 ) ^ { 2 } - ( 3 y ) ^ { 2 } = x ^ { 2 } + 4 x + 4 - 9 y ^ { 2 } $。
14. (8分)先化简,再求值:
(1) $ (2+x)(2-x)+(x-1)(x+5) $,其中$ x= \frac{3}{2} $。化简结果为
(2) $ (2 a-b)^{2}-(4 a+b)(a-b)-2 b^{2} $,其中$ a= \frac{1}{2}, b= -\frac{1}{3} $。化简结果为
(1) $ (2+x)(2-x)+(x-1)(x+5) $,其中$ x= \frac{3}{2} $。化简结果为
4x - 1
,值为5
。(2) $ (2 a-b)^{2}-(4 a+b)(a-b)-2 b^{2} $,其中$ a= \frac{1}{2}, b= -\frac{1}{3} $。化简结果为
-ab
,值为$\frac{1}{6}$
。
答案:
解析
(1) $ ( 2 + x ) ( 2 - x ) + ( x - 1 ) ( x + 5 ) = 4 - x ^ { 2 } + x ^ { 2 } + 5 x - x - 5 = 4 x - 1 $,当 $ x = \frac { 3 } { 2 } $ 时,原式 $ = 4 \times \frac { 3 } { 2 } - 1 = 5 $。
(2) $ ( 2 a - b ) ^ { 2 } - ( 4 a + b ) ( a - b ) - 2 b ^ { 2 } = 4 a ^ { 2 } - 4 a b + b ^ { 2 } - ( 4 a ^ { 2 } - 3 a b - b ^ { 2 } ) - 2 b ^ { 2 } = 4 a ^ { 2 } - 4 a b + b ^ { 2 } - 4 a ^ { 2 } + 3 a b + b ^ { 2 } - 2 b ^ { 2 } = - a b $,当 $ a = \frac { 1 } { 2 } $,$ b = - \frac { 1 } { 3 } $ 时,原式 $ = - \frac { 1 } { 2 } \times \left( - \frac { 1 } { 3 } \right) = \frac { 1 } { 6 } $。
(1) $ ( 2 + x ) ( 2 - x ) + ( x - 1 ) ( x + 5 ) = 4 - x ^ { 2 } + x ^ { 2 } + 5 x - x - 5 = 4 x - 1 $,当 $ x = \frac { 3 } { 2 } $ 时,原式 $ = 4 \times \frac { 3 } { 2 } - 1 = 5 $。
(2) $ ( 2 a - b ) ^ { 2 } - ( 4 a + b ) ( a - b ) - 2 b ^ { 2 } = 4 a ^ { 2 } - 4 a b + b ^ { 2 } - ( 4 a ^ { 2 } - 3 a b - b ^ { 2 } ) - 2 b ^ { 2 } = 4 a ^ { 2 } - 4 a b + b ^ { 2 } - 4 a ^ { 2 } + 3 a b + b ^ { 2 } - 2 b ^ { 2 } = - a b $,当 $ a = \frac { 1 } { 2 } $,$ b = - \frac { 1 } { 3 } $ 时,原式 $ = - \frac { 1 } { 2 } \times \left( - \frac { 1 } { 3 } \right) = \frac { 1 } { 6 } $。
15. 「2025浙江宁波外国语学校质检」(10分)
(1) 代数式$ (s-2 t)(s+2 t+1)+4 t\left(t+\frac{1}{2}\right) 的值与 s, t $的取值有关系吗?请说明理由.
(2) 已知多项式$ a x-b 与 2 x^{2}-x+2 的乘积展开式中不含 x $的一次项,且常数项为$ -4 $,试求$ a^{b} $的值.
(1) 代数式$ (s-2 t)(s+2 t+1)+4 t\left(t+\frac{1}{2}\right) 的值与 s, t $的取值有关系吗?请说明理由.
(2) 已知多项式$ a x-b 与 2 x^{2}-x+2 的乘积展开式中不含 x $的一次项,且常数项为$ -4 $,试求$ a^{b} $的值.
答案:
解析
(1) 代数式的值与 $ t $ 的取值没有关系,与 $ s $ 的取值有关系。理由如下:$ \because ( s - 2 t ) ( s + 2 t + 1 ) + 4 t \left( t + \frac { 1 } { 2 } \right) = s ^ { 2 } + 2 s t + s - 2 s t - 4 t ^ { 2 } - 2 t + 4 t ^ { 2 } + 2 t = s ^ { 2 } + s $,$ \therefore $ 代数式的值与 $ t $ 的取值没有关系,与 $ s $ 的取值有关系。
(2) $ ( a x - b ) ( 2 x ^ { 2 } - x + 2 ) = 2 a x ^ { 3 } - a x ^ { 2 } + 2 a x - 2 b x ^ { 2 } + b x - 2 b = 2 a x ^ { 3 } - ( a + 2 b ) x ^ { 2 } + ( 2 a + b ) x - 2 b $,$ \because $ 展开式中不含 $ x $ 的一次项,且常数项为 -4,$ \therefore 2 a + b = 0 $,$ - 2 b = - 4 $,$ \therefore a = - 1 $,$ b = 2 $。$ \therefore a ^ { b } = 1 $。
(1) 代数式的值与 $ t $ 的取值没有关系,与 $ s $ 的取值有关系。理由如下:$ \because ( s - 2 t ) ( s + 2 t + 1 ) + 4 t \left( t + \frac { 1 } { 2 } \right) = s ^ { 2 } + 2 s t + s - 2 s t - 4 t ^ { 2 } - 2 t + 4 t ^ { 2 } + 2 t = s ^ { 2 } + s $,$ \therefore $ 代数式的值与 $ t $ 的取值没有关系,与 $ s $ 的取值有关系。
(2) $ ( a x - b ) ( 2 x ^ { 2 } - x + 2 ) = 2 a x ^ { 3 } - a x ^ { 2 } + 2 a x - 2 b x ^ { 2 } + b x - 2 b = 2 a x ^ { 3 } - ( a + 2 b ) x ^ { 2 } + ( 2 a + b ) x - 2 b $,$ \because $ 展开式中不含 $ x $ 的一次项,且常数项为 -4,$ \therefore 2 a + b = 0 $,$ - 2 b = - 4 $,$ \therefore a = - 1 $,$ b = 2 $。$ \therefore a ^ { b } = 1 $。
16. 「2025河南郑州联考」(13分)我们将$ (a+b)^{2}= a^{2}+2 a b+b^{2} $进行变形,如:$ a^{2}+b^{2}= (a+b)^{2}-2 a b, a b= \frac{(a+b)^{2}-\left(a^{2}+b^{2}\right)}{2} $等.根据以上变形解决下列问题:
(1) 已知$ a^{2}+b^{2}= 8,(a+b)^{2}= 48 $,则$ a b= $______
(2) 若$ x 满足 (25-x)(x-10)= -15 $,求$ (25-x)^{2}+(x-10)^{2} $的值.
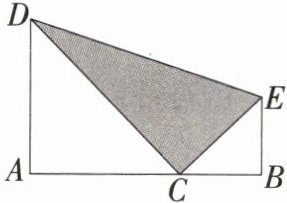
(3) 如图,四边形$ A B E D $是梯形,$ D A \perp A B, E B \perp A B, A D= A C, B E= B C $,连接$ C D, C E $.若$ A C \cdot B C= 10 $,求图中阴影部分的面积.
(1) 已知$ a^{2}+b^{2}= 8,(a+b)^{2}= 48 $,则$ a b= $______
20
.(2) 若$ x 满足 (25-x)(x-10)= -15 $,求$ (25-x)^{2}+(x-10)^{2} $的值.
255
(3) 如图,四边形$ A B E D $是梯形,$ D A \perp A B, E B \perp A B, A D= A C, B E= B C $,连接$ C D, C E $.若$ A C \cdot B C= 10 $,求图中阴影部分的面积.
10

答案:
解析
(1) $ \because a ^ { 2 } + b ^ { 2 } = 8 $,$ ( a + b ) ^ { 2 } = 48 $,$ \therefore a b = \frac { ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) } { 2 } = \frac { 48 - 8 } { 2 } = 20 $。故答案为 20。
(2) $ \because a ^ { 2 } + b ^ { 2 } = ( a + b ) ^ { 2 } - 2 a b $,$ \therefore ( 25 - x ) ^ { 2 } + ( x - 10 ) ^ { 2 } = [ ( 25 - x ) + ( x - 10 ) ] ^ { 2 } - 2 ( 25 - x ) ( x - 10 ) = 15 ^ { 2 } - 2 \times ( - 15 ) = 225 + 30 = 255 $。
(3) 设 $ A D = A C = a $,$ B E = B C = b $,则题图中阴影部分的面积为 $ \frac { 1 } { 2 } ( a + b ) ( a + b ) - \frac { 1 } { 2 } ( a ^ { 2 } + b ^ { 2 } ) = \frac { 1 } { 2 } [ ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) ] = \frac { 1 } { 2 } \times 2 a b = a b = 10 $。
(1) $ \because a ^ { 2 } + b ^ { 2 } = 8 $,$ ( a + b ) ^ { 2 } = 48 $,$ \therefore a b = \frac { ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) } { 2 } = \frac { 48 - 8 } { 2 } = 20 $。故答案为 20。
(2) $ \because a ^ { 2 } + b ^ { 2 } = ( a + b ) ^ { 2 } - 2 a b $,$ \therefore ( 25 - x ) ^ { 2 } + ( x - 10 ) ^ { 2 } = [ ( 25 - x ) + ( x - 10 ) ] ^ { 2 } - 2 ( 25 - x ) ( x - 10 ) = 15 ^ { 2 } - 2 \times ( - 15 ) = 225 + 30 = 255 $。
(3) 设 $ A D = A C = a $,$ B E = B C = b $,则题图中阴影部分的面积为 $ \frac { 1 } { 2 } ( a + b ) ( a + b ) - \frac { 1 } { 2 } ( a ^ { 2 } + b ^ { 2 } ) = \frac { 1 } { 2 } [ ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) ] = \frac { 1 } { 2 } \times 2 a b = a b = 10 $。
查看更多完整答案,请扫码查看


