《2025年5年中考3年模拟八年级数学上册人教版》

11.「★☆」已知 $ m $ 为有理数,则整式 $ m^{2}(m^{2}-1)-m^{2}+1 $ 的值(A)
A. 不是负数
B. 恒为负数
C. 恒为正数
D. 不等于 0

答案： A 原式 $ = m ^ { 2 } ( m ^ { 2 } - 1 ) - ( m ^ { 2 } - 1 ) = ( m ^ { 2 } - 1 ) ^ { 2 } \geq 0 $，即整式 $ m ^ { 2 } ( m ^ { 2 } - 1 ) - m ^ { 2 } + 1 $ 的值不是负数，故选 A.

12.「★☆」下列何者为多项式 $ 5x(5x - 2)-4(5x - 2)^{2} $ 的因式分解？(C)
A. $ (5x - 2)(25x - 8) $
B. $ (5x - 2)(5x - 4) $
C. $ (5x - 2)(-15x + 8) $
D. $ (5x - 2)(-20x + 4) $

答案： C $ 5 x ( 5 x - 2 ) - 4 ( 5 x - 2 ) ^ { 2 } = ( 5 x - 2 ) [ 5 x - 4 ( 5 x - 2 ) ] = ( 5 x - 2 ) ( - 15 x + 8 ) $. 故选 C.

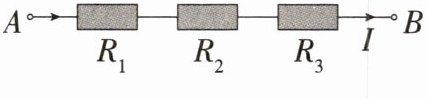
13. 跨学科 串联电路「2025安徽芜湖一中期末,★☆」如图,把 $ R_{1} $,$ R_{2} $,$ R_{3} $ 三个电阻串联起来,线路 $ AB $ 上的电流为 $ I $,电压为 $ U $,则 $ U = IR_{1}+IR_{2}+IR_{3} $,当 $ R_{1}= 18.4 $,$ R_{2}= 16.7 $,$ R_{3}= 20.9 $,$ I = 3.5 $ 时,$ U $ 的值为

196.

答案： 答案 196
解析 把 $ R _ { 1 } = 18.4 $，$ R _ { 2 } = 16.7 $，$ R _ { 3 } = 20.9 $，$ I = 3.5 $ 代入 $ U = I R _ { 1 } + I R _ { 2 } + I R _ { 3 } $，得 $ U = 18.4 \times 3.5 + 16.7 \times 3.5 + 20.9 \times 3.5 = ( 18.4 + 16.7 + 20.9 ) \times 3.5 = 196 $，故答案为 196.

14.「2025广东深圳模拟,★☆」已知 $ (2x - 21)(3x - 7)-(3x - 7)(x - 13) $ 可分解因式为 $ (3x + a)(x + b) $,其中 $ a,b $ 均为整数,则 $ a + 3b $ 的值为-31.

答案： 答案 $ - 31 $
解析 $ ( 2 x - 21 ) ( 3 x - 7 ) - ( 3 x - 7 ) ( x - 13 ) = ( 3 x - 7 ) \cdot ( 2 x - 21 - x + 13 ) = ( 3 x - 7 ) ( x - 8 ) $，$ \because ( 2 x - 21 ) ( 3 x - 7 ) - ( 3 x - 7 ) ( x - 13 ) $ 可分解因式为 $ ( 3 x + a ) ( x + b ) $，$ \therefore ( 3 x - 7 ) ( x - 8 ) = ( 3 x + a ) ( x + b ) $，则 $ a = - 7 $，$ b = - 8 $，故 $ a + 3 b = - 7 + 3 \times ( - 8 ) = - 31 $. 故答案为 $ - 31 $.

15.「★☆」设 $ a = 4046 - 2022×2+301 $,$ b = 2023×2024 - 2021×2025 $,则 $ a,b $ 的大小关系为______b＞a.(用“＞”连接)

答案： 答案 $ b ＞ a $
解析 $ a = 2 \times ( 2023 - 2022 ) + 301 = 303 $，
$ b = 2023 \times ( 2023 + 1 ) - ( 2023 - 2 ) \times ( 2023 + 2 ) = 2023 ^ { 2 } + 2023 - 2023 ^ { 2 } + 4 = 2027 $，
$ \because 2027 ＞ 303 $，$ \therefore b ＞ a $.

16.「2025湖南娄底质检,★☆」因式分解：
(1) $ 2x(a - b)+3y(b - a) $.
(2) $ x(x^{2}-xy)-(4x^{2}-4xy) $.
(3) $ 3(x + y)(x - y)-(x - y)^{2} $.
(4) $ 2ab^{2}-6a^{2}b^{2}+4a^{3}b^{2} $.

答案： 解析
(1) 原式 $ = 2 x ( a - b ) - 3 y ( a - b ) $
$ = ( a - b ) ( 2 x - 3 y ) $.
(2) 原式 $ = x ^ { 2 } ( x - y ) - 4 x ( x - y ) = x ( x - y ) ( x - 4 ) $.
(3) 原式 $ = ( x - y ) [ 3 ( x + y ) - ( x - y ) ] $
$ = ( x - y ) ( 3 x + 3 y - x + y ) $
$ = ( x - y ) ( 2 x + 4 y ) $
$ = 2 ( x - y ) ( x + 2 y ) $.
(4) 原式 $ = 2 a b ^ { 2 } ( 1 - 3 a + 2 a ^ { 2 } ) $
$ = 2 a b ^ { 2 } [ ( 1 - a ) - 2 a ( 1 - a ) ] $
$ = 2 a b ^ { 2 } ( 2 a - 1 ) ( a - 1 ) $.

17. 新课标 新题型 运算能力 阅读理解题 把多项式 $ am + an+bm + bn $ 分解因式.
解法一：$ am + an+bm + bn= (am + an)+(bm + bn)= a(m + n)+b(m + n)= (m + n)(a + b) $.
解法二：$ am + an+bm + bn= (am + bm)+(an + bn)= m(a + b)+n(a + b)= (m + n)(a + b) $.
(1) 分解因式：$ m^{2}x - 3m+mnx - 3n $=$ m ( m x - 3 ) + n ( m x - 3 ) = ( m x - 3 ) ( m + n ) $.
(2) 已知 $ a,b,c $ 为 $ △ABC $ 的三边长,且 $ a^{3}-a^{2}b+5ac - 5bc = 0 $,试判断 $ △ABC $ 的形状.$ \because a ^ { 3 } - a ^ { 2 } b + 5 a c - 5 b c = 0 $，$ \therefore a ^ { 2 } ( a - b ) + 5 c ( a - b ) = 0 $，$ \therefore ( a - b ) ( a ^ { 2 } + 5 c ) = 0 $，$ \because a $，$ b $，$ c $ 为 $ \triangle A B C $ 的三边长，$ \therefore a ^ { 2 } + 5 c \neq 0 $，$ \therefore a - b = 0 $，$ \therefore a = b $，$ \therefore \triangle A B C $ 是等腰三角形.

答案： 解析
(1) 原式 $ = m ( m x - 3 ) + n ( m x - 3 ) $
$ = ( m x - 3 ) ( m + n ) $.
(2) $ \because a ^ { 3 } - a ^ { 2 } b + 5 a c - 5 b c = 0 $，
$ \therefore a ^ { 2 } ( a - b ) + 5 c ( a - b ) = 0 $，$ \therefore ( a - b ) ( a ^ { 2 } + 5 c ) = 0 $，
$ \because a $，$ b $，$ c $ 为 $ \triangle A B C $ 的三边长，$ \therefore a ^ { 2 } + 5 c \neq 0 $，
$ \therefore a - b = 0 $，$ \therefore a = b $，$ \therefore \triangle A B C $ 是等腰三角形.

18. 新课标 运算能力 阅读下列因式分解的过程,再回答所提出的问题.
$ (x + 1)+x(x + 1)+x(x + 1)^{2}= (1 + x)[1 + x+x(x + 1)]= (1 + x)^{2}(1 + x)= (1 + x)^{3} $.
(1) 上述因式分解的方法是提公因式法,共应用了2次.
(2) 若分解因式 $ 1 + x+x(x + 1)+x(x + 1)^{2}+…+x(x + 1)^{2025} $,则需应用上述方法2025次,结果是$(1 + x)^{2026}$.
(3) 分解因式：$ 1 + x+x(x + 1)+x(x + 1)^{2}+…+x(x + 1)^{n} $($ n $ 为正整数).
$(1 + x)^{n+1}$

答案： 解析
(1) 提公因式法；2.
(2) 2025；$ ( 1 + x ) ^ { 2026 } $.
(3) 由
(1) 和
(2) 知，最终分解因式的结果的次数是原式最高次数加 1，
$ \therefore 1 + x + x ( x + 1 ) + x ( x + 1 ) ^ { 2 } + \cdots + x ( x + 1 ) ^ { n } $
$ = ( 1 + x ) ^ { n + 1 } $.