第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025 浙江台州期末」给出下列长度的三条线段,能组成三角形的是 (
A.2,3,5
B.6,7,15
C.3,4,5
D.5,5,11
C
)A.2,3,5
B.6,7,15
C.3,4,5
D.5,5,11
答案:
C 因为 $2 + 3 = 5$,$6 + 7 < 15$,$3 + 4 > 5$,$5 + 5 < 11$,所以选项A、B、D中的三条线段不能组成三角形,只有选项C中的三条线段能组成三角形,故选C.
2.「2024 江苏淮安中考」用一根小木棒与两根长度分别为 3 cm,5 cm 的小木棒组成三角形,则这根小木棒的长度可以是 (
A.9 cm
B.7 cm
C.2 cm
D.1 cm
B
)A.9 cm
B.7 cm
C.2 cm
D.1 cm
答案:
B 设这根小木棒的长度为 $x$ cm,由三角形的三边关系得 $5 - 3 < x < 5 + 3$,所以 $x$ 的取值范围是 $2 < x < 8$,观察选项,只有选项B符合题意.故选B.
3.满足下列条件的三条线段 a,b,c 能组成三角形的是 (
A.a:b:c = 1:2:3
B.a + b = 4,a + b + c = 9
C.a = 7,b = 9,c = 12
D.a = 3t,b = 2t,c = t
C
)A.a:b:c = 1:2:3
B.a + b = 4,a + b + c = 9
C.a = 7,b = 9,c = 12
D.a = 3t,b = 2t,c = t
答案:
C A.设 $a$ 的长度为 $x$,则 $b$,$c$ 的长度为 $2x$,$3x$,则有 $a + b = c$,不符合三角形任意两边之和大于第三边的条件,故该选项不符合题意;B. $\because a + b = 4$,$a + b + c = 9$,$\therefore c = 5$,$\because 4 < 5$,$\therefore$ 不符合三角形任意两边之和大于第三边的条件,故该选项不符合题意;C. $a = 7$,$b = 9$,$c = 12$,$7 + 9 > 12$,故该选项符合题意;D. $a = 3t$,$b = 2t$,$c = t$,则 $c + b = a$,不符合三角形任意两边之和大于第三边的条件,故该选项不符合题意.故选C.
技巧点拨 只要满足三条线段中较短的两条线段之和大于第三条线段的条件,这三条线段就能构成三角形.
技巧点拨 只要满足三条线段中较短的两条线段之和大于第三条线段的条件,这三条线段就能构成三角形.
4.如图,数轴上 A,B 两点到原点的距离是某三角形两边的长,则该三角形第三边长不可能是 (
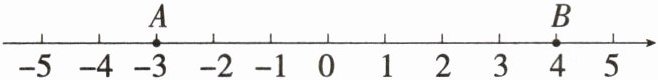
A.2
B.4
C.6
D.8
D
)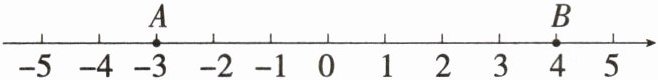
A.2
B.4
C.6
D.8
答案:
D 由数轴可得,$A$ 到原点的距离为 $3$,$B$ 到原点的距离为 $4$,设该三角形第三边长为 $x$,则 $x$ 的取值范围是 $1 < x < 7$,$\therefore$ 该三角形第三边长不可能是 $8$.故选D.
5.学用教材特色变式 用一条长为 15 cm 的细绳围成一个等腰三角形.
(1)设等腰三角形的腰长为 a cm,求 a 的取值范围.
(2)若等腰三角形的一边长为 3 cm,求另两边长.
(1)设等腰三角形的腰长为 a cm,求 a 的取值范围.
(2)若等腰三角形的一边长为 3 cm,求另两边长.
答案:
解析
(1) $\because$ 腰长为 $a$ cm,周长为 $15$ cm,$\therefore$ 底边长为 $(15 - 2a)$ cm,$\therefore a + a > 15 - 2a$,$15 - 2a > 0$,$\therefore \frac{15}{4} < a < \frac{15}{2}$.
(2) ①当 $3$ cm 为底边长时,腰长为 $6$ cm,$6 + 3 > 6$,能组成三角形.
②当 $3$ cm 为腰长时,底边长为 $9$ cm,$3 + 3 < 9$,不能组成三角形.
故另两边长分别为 $6$ cm,$6$ cm.
(1) $\because$ 腰长为 $a$ cm,周长为 $15$ cm,$\therefore$ 底边长为 $(15 - 2a)$ cm,$\therefore a + a > 15 - 2a$,$15 - 2a > 0$,$\therefore \frac{15}{4} < a < \frac{15}{2}$.
(2) ①当 $3$ cm 为底边长时,腰长为 $6$ cm,$6 + 3 > 6$,能组成三角形.
②当 $3$ cm 为腰长时,底边长为 $9$ cm,$3 + 3 < 9$,不能组成三角形.
故另两边长分别为 $6$ cm,$6$ cm.
6.「2025 贵州铜仁期中」如图,一扇窗户打开后,用窗钩 AB 可将其固定,这里所运用的几何原理是 (
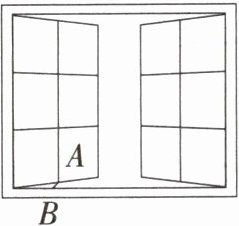
A.三角形的内角和等于 180°
B.两点之间,线段最短
C.两点确定一条直线
D.三角形具有稳定性
D
)
A.三角形的内角和等于 180°
B.两点之间,线段最短
C.两点确定一条直线
D.三角形具有稳定性
答案:
D 用窗钩将打开的窗户固定,这样就形成了一个三角形,所以所运用的几何原理是三角形具有稳定性,故选D.
7.新考向结论开放题 六边形钢架 ABCDEF 由 6 条钢管铰接而成,如图所示,为使这一钢架稳固,试用三条钢管连接使之不能活动,方法很多,请至少画出三种方法.(只需画图,不必写出作法)
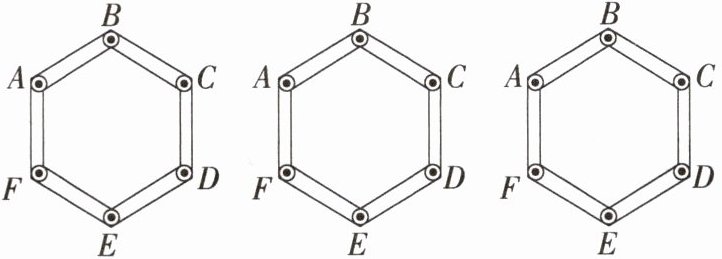

答案:
解析 如图所示.(答案不唯一)

解析 如图所示.(答案不唯一)

8.「2025 内蒙古乌兰察布期中,★☆」如图,下面的四个盒子中,每个盒子里都有两根小棒,把其中的一根小棒用剪刀按图中所示的位置剪成两段,这两段小棒再与另一根小棒首尾相接,能够围成一个三角形的是 (
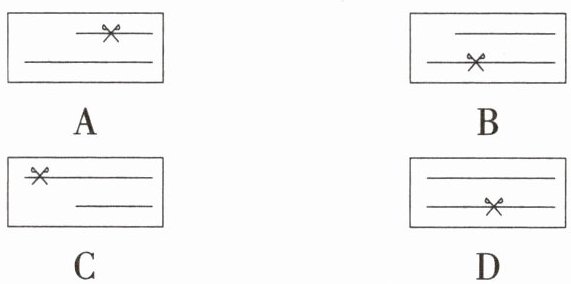
B
)
答案:
B A.图中小棒被剪刀剪成两段,这两段加起来比下面那根小棒短,不符合三角形的三边关系,无法围成三角形;B.图中小棒被剪刀剪成两段,这两段都比上面那根小棒短,且这两段加起来比上面那根小棒长,符合三角形的三边关系,可以围成三角形;C.图中小棒被剪刀剪成两段,这两段相减(较长的减较短的)比下面那根小棒还长,不符合三角形的三边关系,无法围成三角形;D.图中小棒被剪刀剪成两段,这两段加起来和上面那根小棒相等,不符合三角形的三边关系,无法围成三角形.
查看更多完整答案,请扫码查看


