《2025年5年中考3年模拟八年级数学上册人教版》

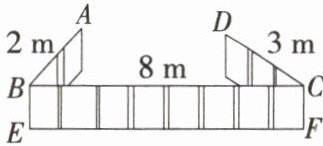
9.「2025 湖北荆州月考,★☆」为方便劳动技术小组实践教学,需用篱笆围一块三角形空地,现已连接好三段篱笆 AB,BC,CD,这三段篱笆的长度如图所示,其中篱笆 AB,CD 可分别绕轴 BE 和 CF 转动.若要围成一个三角形的空地,则在篱笆 CD 上接上新的篱笆的长度可以为 (B)

A.3 m
B.4 m
C.8 m
D.9 m

答案： B 由题图可知 $BC = 8$ m，$AB = 2$ m，$CD = 3$ m，设在篱笆 $CD$ 上接上新的篱笆的长度为 $x$ m，若要围成一个三角形的空地，则 $8 - 2 ＜ 3 + x ＜ 8 + 2$，解得 $3 ＜ x ＜ 7$，故选B.

10.「2025 福建厦门集美期中,★☆」某中学九年级(2)班学生杨冲家和李锐家到学校的直线距离分别是 5 km 和 3 km,那么杨冲,李锐两家的直线距离不可能是 (A)
A.1 km
B.2 km
C.3 km
D.8 km

答案： A 当杨冲，李锐两家和学校都在一条直线上时，杨冲，李锐两家的直线距离为 $2$ km 或 $8$ km，当杨冲家，李锐家和学校不在一条直线上时，设杨冲，李锐两家的直线距离为 $x$ km，根据三角形的三边关系得 $5 - 3 ＜ x ＜ 5 + 3$，即 $2 ＜ x ＜ 8$，故杨冲，李锐两家的直线距离可能为 $3$ km，故B、C、D均不符合题意，故选A.

11.新考向结论开放题 「2024 青海西宁中考,★☆」若长度分别为 3,6,a 的三条线段能组成一个三角形,则整数 a 的值可以是____4.(写出一个即可)

答案： 答案 $4$（答案不唯一）
解析 $\because$ 长度分别为 $3$，$6$，$a$ 的三条线段能组成一个三角形，$\therefore 6 - 3 ＜ a ＜ 6 + 3$，$\therefore 3 ＜ a ＜ 9$，$\therefore$ 整数 $a$ 的值可以是 $4$（答案不唯一）.

12.「2024 江苏徐州联考,★☆」若实数 m,n 满足|m - 2| + √(n - 4) = 0,且 m,n 恰好是等腰△ABC 的两条边的边长,则△ABC 的周长是10.

答案： 答案 $10$
解析 $\because |m - 2| + \sqrt{n - 4} = 0$，$\therefore m - 2 = 0$，$n - 4 = 0$，解得 $m = 2$，$n = 4$，当 $2$ 为腰长时，$2 + 2 = 4$，不符合三角形的三边关系；当 $4$ 为腰长时，$2 + 4 ＞ 4$，符合三角形的三边关系，周长为 $2 + 4 + 4 = 10$.故答案为 $10$.

13.「2025 北京实验学校期中,★☆」三个数 3a - 21,2a - 10,3a - 16 所对应的点在数轴上从左到右依次排列,三个数均大于 0,且以这三个数为边长能构成三角形,则整数 a 的值为8 或 9 或 10.

答案： 答案 $8$ 或 $9$ 或 $10$
解析 $\because 3a - 21$，$2a - 10$，$3a - 16$ 所对应的点在数轴上从左到右依次排列，$\therefore 3a - 21 ＜ 2a - 10 ＜ 3a - 16$，$\therefore 6 ＜ a ＜ 11$，$\because$ 以这三个数为边长能构成三角形，$\therefore 3a - 21 + 2a - 10 ＞ 3a - 16$，$\therefore a ＞ 7.5$，$\therefore 7.5 ＜ a ＜ 11$，$\therefore$ 整数 $a$ 的值为 $8$ 或 $9$ 或 $10$.

14.「2025 黑龙江哈尔滨月考,★☆」已知 a,b,c 分别为△ABC 的三边长(a ＞ b),且满足 a + b = 3c - 2,a - b = 2c - 6.
(1)求 c 的取值范围.1＜c＜6
(2)若△ABC 的周长为 14,求 c 的值,并判断△ABC 的形状.4，△ABC 是等腰三角形.

答案： 解析
(1) $\because a$，$b$，$c$ 分别为 $\triangle ABC$ 的三边长 $(a ＞ b)$，且满足 $a + b = 3c - 2$，$a - b = 2c - 6$，$\therefore a + b = 3c - 2 ＞ c$，$a - b = 2c - 6 ＜ c$，$\therefore \left\{\begin{array}{l}3c - 2 ＞ c\\2c - 6 ＜ c\end{array}\right.$，解得 $1 ＜ c ＜ 6$，$\therefore c$ 的取值范围为 $1 ＜ c ＜ 6$.
(2) 由题意知，$a + b + c = 3c - 2 + c = 14$，解得 $c = 4$，则 $\left\{\begin{array}{l}a + b = 10\\a - b = 2\end{array}\right.$，解得 $\left\{\begin{array}{l}a = 6\\b = 4\end{array}\right.$，$\therefore b = c$，$\therefore \triangle ABC$ 是等腰三角形.

15.「2025 安徽安庆期末,★☆」已知 a,b,c 是△ABC 的三边长.
(1)化简:|a - b + c| + |a - b - c|.2c
(2)若 a 和 b 满足方程组 { a + 2b = 12, 2a - b = -1, } 且 c 为偶数,求这个三角形的周长.11 或 13

答案： 解析
(1) $\because a$，$b$，$c$ 是 $\triangle ABC$ 的三边长，$\therefore a + c ＞ b$，$b + c ＞ a$，$\therefore a - b + c ＞ 0$，$a - b - c ＜ 0$，$\therefore |a - b + c| + |a - b - c| = (a - b + c) - (a - b - c) = a - b + c - a + b + c = 2c$.
(2) 解方程组 $\left\{\begin{array}{l}a + 2b = 12\\2a - b = -1\end{array}\right.$ 得 $\left\{\begin{array}{l}a = 2\\b = 5\end{array}\right.$，根据三角形的三边关系得 $5 - 2 ＜ c ＜ 2 + 5$，即 $3 ＜ c ＜ 7$，$\because c$ 为偶数，$\therefore c = 4$ 或 $6$，当 $c = 4$ 时，三角形的周长为 $2 + 5 + 4 = 11$；当 $c = 6$ 时，三角形的周长为 $2 + 5 + 6 = 13$. $\therefore$ 这个三角形的周长为 $11$ 或 $13$.

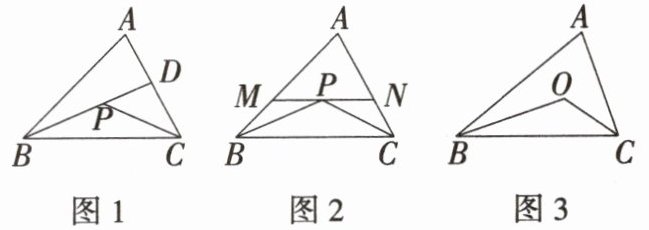
16.新课标推理能力 「2024 湖北鄂州期中」有一道题如下:
如图 1,填空:
由三角形两边的和大于第三边,得 AB + AD ＞BD,PD + CD ＞PC.将不等式左边、右边分别相加,得 AB + AD + PD + CD ＞BD + PC,即 AB + AC ＞BP + PC.
(1)补全横线上的内容.
(2)仿照所给方法,请你利用图 2(M,N,P 三点共线)证明 AB + AC ＞ PB + PC.
(3)如图 3,点 O 是△ABC 内一点,连接 OB 和 OC.若 AB = 6,AC = 5,BC = 7,你能写出 OB + OC 的取值范围吗?
7＜BO+CO＜11

答案： 解析
(1) $BD$；$PC$；$BD + PC$；$BP + PC$.
(2) 证明：在 $\triangle AMN$ 中，$AM + AN ＞ MN$，在 $\triangle MPB$ 中，$MP + MB ＞ BP$，在 $\triangle NPC$ 中，$NP + NC ＞ PC$，将三个不等式左边、右边分别相加得 $AM + AN + MB + MP + PN + NC ＞ MP + NP + PB + PC$，即 $AB + AC ＞ PB + PC$.
(3) 根据三角形的三边关系可得 $BO + CO ＞ BC$，易得 $BO + CO ＜ AB + AC$，$\because AB = 6$，$AC = 5$，$BC = 7$，$\therefore 7 ＜ BO + CO ＜ 11$.