第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 教材特色变式「2025山东济南期中」如图,在$\triangle ABC和\triangle DEF$中,$AB= DE,AC= DF$,要利用“SSS”判定$\triangle ABC\cong \triangle DEF$,则可添加的条件为(
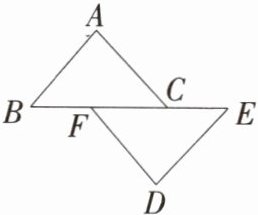
A.$BF= CF$
B.$BF= CE$
C.$CF= CE$
D.$∠A= ∠D$
B
)
A.$BF= CF$
B.$BF= CE$
C.$CF= CE$
D.$∠A= ∠D$
答案:
B
∵在△ABC和△DEF中,AB = DE,AC = DF,
∴利用“SSS”判定△ABC≌△DEF需添加的条件是BC = EF,又当BF = CE时,BF + CF = EC + CF,即BC = EF,
∴可添加条件BF = CE。故选B。
∵在△ABC和△DEF中,AB = DE,AC = DF,
∴利用“SSS”判定△ABC≌△DEF需添加的条件是BC = EF,又当BF = CE时,BF + CF = EC + CF,即BC = EF,
∴可添加条件BF = CE。故选B。
2.「2024四川内江中考改编」如图,点A,D,B,E在同一条直线上,$AD= BE,AC= DF,BC= EF$.若$∠A= 55^{\circ },∠E= 45^{\circ }$,则$∠F$的度数为____

80°
.
答案:
答案 80°
解析
∵AD = BE,
∴AD + BD = BE + BD,即AB = DE,在△ABC和△DEF中,$\left\{\begin{array}{l}AB = DE,\\AC = DF,\\BC = EF,\end{array}\right.$
∴△ABC≌△DEF(SSS),
∴∠A = ∠FDE = 55°,
∴∠F = 180° - (∠FDE + ∠E) = 180° - (55° + 45°) = 80°。
解析
∵AD = BE,
∴AD + BD = BE + BD,即AB = DE,在△ABC和△DEF中,$\left\{\begin{array}{l}AB = DE,\\AC = DF,\\BC = EF,\end{array}\right.$
∴△ABC≌△DEF(SSS),
∴∠A = ∠FDE = 55°,
∴∠F = 180° - (∠FDE + ∠E) = 180° - (55° + 45°) = 80°。
3.「2023西藏中考」如图,已知$AB= DE,AC= DC,CE= CB$.求证:$∠1= ∠2$.
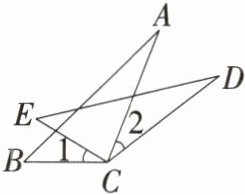
证明 在△ABC和△DEC中,$\left\{\begin{array}{l}AB = DE,\\AC = DC,\\CB = CE,\end{array}\right.$
∴△ABC≌△DEC(
∴∠ACB = ∠DCE,
∴∠ACB - ∠ACE = ∠DCE - ∠ACE,∴∠1 = ∠2。

证明 在△ABC和△DEC中,$\left\{\begin{array}{l}AB = DE,\\AC = DC,\\CB = CE,\end{array}\right.$
∴△ABC≌△DEC(
SSS
),∴∠ACB = ∠DCE,
∴∠ACB - ∠ACE = ∠DCE - ∠ACE,∴∠1 = ∠2。
答案:
证明 在△ABC和△DEC中,$\left\{\begin{array}{l}AB = DE,\\AC = DC,\\CB = CE,\end{array}\right.$
∴△ABC≌△DEC(SSS),
∴∠ACB = ∠DCE,
∴∠ACB - ∠ACE = ∠DCE - ∠ACE,
∴∠1 = ∠2。
∴△ABC≌△DEC(SSS),
∴∠ACB = ∠DCE,
∴∠ACB - ∠ACE = ∠DCE - ∠ACE,
∴∠1 = ∠2。
4.「2025重庆渝北月考」如图,已知$AB= AD,BC= DE,AC= AE,∠1= 42^{\circ }$,求$∠2$的度数.

∠2的度数为

∠2的度数为
42°
.
答案:
解析
∵在△ABC和△ADE中,$\left\{\begin{array}{l}AB = AD,\\BC = DE,\\AC = AE,\end{array}\right.$
∴△ABC≌△ADE(SSS),
∴∠ADE = ∠B,
∵∠1 + ∠B + ∠ADB = 180°,∠2 + ∠ADE + ∠ADB = 180°,
∴∠2 = ∠1 = 42°。
∵在△ABC和△ADE中,$\left\{\begin{array}{l}AB = AD,\\BC = DE,\\AC = AE,\end{array}\right.$
∴△ABC≌△ADE(SSS),
∴∠ADE = ∠B,
∵∠1 + ∠B + ∠ADB = 180°,∠2 + ∠ADE + ∠ADB = 180°,
∴∠2 = ∠1 = 42°。
5.「2025广东深圳联考,」如图,在四边形ABCD中,对角线AC,BD相交于点O.已知$AD= BC,AC= BD$,若$∠ACD= 30^{\circ }$,则$∠AOD$的度数为(
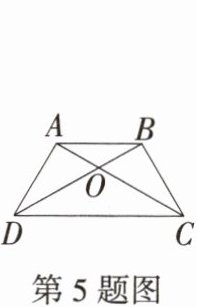
A.$50^{\circ }$
B.$60^{\circ }$
C.$70^{\circ }$
D.$80^{\circ }$
B
)
A.$50^{\circ }$
B.$60^{\circ }$
C.$70^{\circ }$
D.$80^{\circ }$
答案:
B 在△ACD和△BDC中,$\left\{\begin{array}{l}AD = BC,\\DC = CD,\\AC = DB,\end{array}\right.$
∴△ACD≌△BDC(SSS),
∴∠ACD = ∠BDC = 30°,
∴∠AOD = ∠ACD + ∠BDC = 30° + 30° = 60°,故选B。
∴△ACD≌△BDC(SSS),
∴∠ACD = ∠BDC = 30°,
∴∠AOD = ∠ACD + ∠BDC = 30° + 30° = 60°,故选B。
6.「2024安徽合肥月考,」如图,$CA= CB,AD= BD$,M,N分别是CA,CB的中点,若$\triangle ADM$的面积为3,则图中阴影部分的面积为____.


答案:
答案 6
解析 如图,连接CD,在△ACD和△BCD中,$\left\{\begin{array}{l}CA = CB,\\CD = CD,\\AD = BD,\end{array}\right.$
∴△ACD≌△BCD(SSS),
∴$S_{\triangle ACD} = S_{\triangle BCD}$,
∵M,N分别是CA,CB的中点,
∴$S_{\triangle ADM} = S_{\triangle CDM} = \frac{1}{2}S_{\triangle ACD}$,$S_{\triangle BDN} = S_{\triangle CDN} = \frac{1}{2}S_{\triangle BCD}$,
∴阴影部分的面积 = 2$S_{\triangle ADM}$ = 2 × 3 = 6。

答案 6
解析 如图,连接CD,在△ACD和△BCD中,$\left\{\begin{array}{l}CA = CB,\\CD = CD,\\AD = BD,\end{array}\right.$
∴△ACD≌△BCD(SSS),
∴$S_{\triangle ACD} = S_{\triangle BCD}$,
∵M,N分别是CA,CB的中点,
∴$S_{\triangle ADM} = S_{\triangle CDM} = \frac{1}{2}S_{\triangle ACD}$,$S_{\triangle BDN} = S_{\triangle CDN} = \frac{1}{2}S_{\triangle BCD}$,
∴阴影部分的面积 = 2$S_{\triangle ADM}$ = 2 × 3 = 6。

7.新考向结论开放题「2025江苏镇江模拟,」如图,已知$AB= AC,AD= AE,BD= CE$,B,D,E三点共线,AC与BE相交于点F,请从结论①$∠ADE= ∠CAE+∠ACE$,②$∠BAC= ∠BEC$中选择一个进行证明.
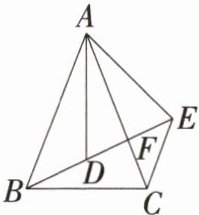
证明 答案不唯一,选择其中一个证明即可。
选择①。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\BD = CE,\\AD = AE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠BAD = ∠CAE,∠ABD = ∠ACE,
∴∠ADE = ∠BAD + ∠ABD = ∠CAE + ∠ACE。
选择②。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\AD = AE,\\BD = CE,\end{array}\right.$
∴△ABD≌△ACE(SSS),∴∠ABD = ∠ACE。
又∵∠AFB = ∠EFC,
∴180° - (∠ABD + ∠AFB) = 180° - (∠ACE + ∠EFC),
∴∠BAC = ∠BEC。

证明 答案不唯一,选择其中一个证明即可。
选择①。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\BD = CE,\\AD = AE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠BAD = ∠CAE,∠ABD = ∠ACE,
∴∠ADE = ∠BAD + ∠ABD = ∠CAE + ∠ACE。
选择②。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\AD = AE,\\BD = CE,\end{array}\right.$
∴△ABD≌△ACE(SSS),∴∠ABD = ∠ACE。
又∵∠AFB = ∠EFC,
∴180° - (∠ABD + ∠AFB) = 180° - (∠ACE + ∠EFC),
∴∠BAC = ∠BEC。
答案:
证明 答案不唯一,选择其中一个证明即可。
选择①。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\BD = CE,\\AD = AE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠BAD = ∠CAE,∠ABD = ∠ACE,
∴∠ADE = ∠BAD + ∠ABD = ∠CAE + ∠ACE。
选择②。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\AD = AE,\\BD = CE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠ABD = ∠ACE。
又
∵∠AFB = ∠EFC,
∴180° - (∠ABD + ∠AFB) = 180° - (∠ACE + ∠EFC),
∴∠BAC = ∠BEC。
选择①。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\BD = CE,\\AD = AE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠BAD = ∠CAE,∠ABD = ∠ACE,
∴∠ADE = ∠BAD + ∠ABD = ∠CAE + ∠ACE。
选择②。
在△ABD和△ACE中,$\left\{\begin{array}{l}AB = AC,\\AD = AE,\\BD = CE,\end{array}\right.$
∴△ABD≌△ACE(SSS),
∴∠ABD = ∠ACE。
又
∵∠AFB = ∠EFC,
∴180° - (∠ABD + ∠AFB) = 180° - (∠ACE + ∠EFC),
∴∠BAC = ∠BEC。
查看更多完整答案,请扫码查看


