《2025年5年中考3年模拟八年级数学上册人教版》

1.「2025 湖北武汉期末」下列整式乘法中,能用平方差公式简便计算的是 (B)
A. $(2a + b)(a - 2b)$
B. $(a + 2b)(2b - a)$
C. $(-a + b)(b - a)$
D. $(-a - b)(a + b)$

答案： B $(2a + b)(a - 2b)$只能利用多项式乘多项式的计算方法进行计算，不能利用平方差公式，因此选项A不符合题意；$(a + 2b)(2b - a) = (2b + a)(2b - a) = 4b^{2} - a^{2}$，能利用平方差公式，因此选项B符合题意；$(-a + b)(b - a) = (b - a)(b - a) = b^{2} - 2ab + a^{2}$，不能利用平方差公式，因此选项C不符合题意；$(-a - b)(a + b) = -(a + b)(a + b) = -a^{2} - 2ab - b^{2}$，不能利用平方差公式，因此选项D不符合题意.故选B.

2. 计算 $(1 - 2x)(1 + 2x)$ 的结果是 (B)
A. $4x^{2} + 1$
B. $1 - 4x^{2}$
C. $4x^{2}$
D. $-4x^{2} - 1$

答案： B $(1 - 2x)(1 + 2x) = 1^{2} - (2x)^{2} = 1 - 4x^{2}$，故选B.

3. 学科教材特色变式 下列运算正确的是 (D)
A. $(x - y)(-x - y) = -x^{2} - y^{2}$
B. $(-1 + xy)(1 + xy) = -1 - x^{2}y^{2}$
C. $(x + y)(x - y) = x^{2} + y^{2}$
D. $(2x + 3)(2x - 3) = 4x^{2} - 9$

答案： D $(x - y)(-x - y) = -(x - y)(x + y) = -(x^{2} - y^{2}) = -x^{2} + y^{2}$，$(-1 + xy)(1 + xy) = x^{2}y^{2} - 1$，$(x + y)(x - y) = x^{2} - y^{2}$，$(2x + 3)(2x - 3) = 4x^{2} - 9$，所以只有D选项运算正确.

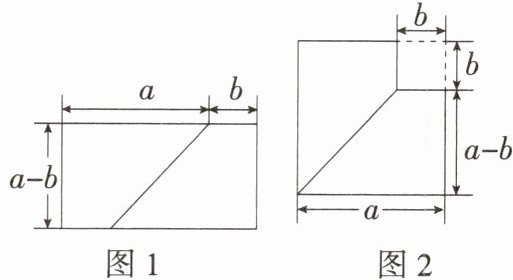
4.「2025 湖北武汉期末」从图 1 到图 2 的变化过程中可以发现的结论是 (B)

A. $(a - b)^{2} = a^{2} - 2ab + b^{2}$
B. $(a + b)(a - b) = a^{2} - b^{2}$
C. $(a + b)^{2} = a^{2} + 2ab + b^{2}$
D. $a^{2} + 2ab + b^{2} = (a + b)^{2}$

答案： B 题图1是长为$a + b$，宽为$a - b$的长方形，因此面积为$(a + b)(a - b)$；题图2中两梯形的面积和=两个正方形的面积差，即$a^{2} - b^{2}$，因此有$(a + b)(a - b) = a^{2} - b^{2}$，故选B.

5. 在横线上添上适当的整式:4x - 3y·$(-4x - 3y) = 9y^{2} - 16x^{2}$.

答案： 答案 $(4x - 3y)$
解析 $9y^{2} - 16x^{2} = (3y + 4x)(3y - 4x) = (-4x - 3y) \cdot (4x - 3y)$.故答案为$(4x - 3y)$.

6.「2025 北京门头沟期末」当 $m^{2} + 2m - 2 = 0$ 时,代数式 $(m + 1)(m - 1) + 2m$ 的值为1.

答案： 答案 1
解析 $\because m^{2} + 2m - 2 = 0$，$\therefore m^{2} + 2m = 2$，$\therefore (m + 1)(m - 1) + 2m = m^{2} - 1 + 2m = 2 - 1 = 1$，故答案为1.

7.「2025 北京丰台期末」计算:
(1) $2a(a - 1) + (a + 3)(a - 3)$.
(2) $(3x + y)(y - 3x) - x(3y - 9x)$.

答案： 解析
(1)$2a(a - 1) + (a + 3)(a - 3)$
$= 2a^{2} - 2a + a^{2} - 9$
$= 3a^{2} - 2a - 9$.
(2)$(3x + y)(y - 3x) - x(3y - 9x) = y^{2} - (3x)^{2} - (3xy - 9x^{2})$
$= y^{2} - 9x^{2} - 3xy + 9x^{2}$
$= y^{2} - 3xy$.

8. 运用平方差公式计算:
(1) $(x + 3)(x - 3)(x^{2} + 9)$.
(2) $(x - \frac{1}{2})(x^{2} + \frac{1}{4})(x + \frac{1}{2})$.

答案： 解析
(1)$(x + 3)(x - 3)(x^{2} + 9) = (x^{2} - 9)(x^{2} + 9) = x^{4} - 81$.
(2)$(x - \frac{1}{2})(x^{2} + \frac{1}{4})(x + \frac{1}{2}) = (x^{2} - \frac{1}{4})(x^{2} + \frac{1}{4})$
$= x^{4} - \frac{1}{16}$.

9. 若 $a = 2022^{0}, b = 2025×2023 - 2024^{2}, c = (-\frac{2}{3})^{2025}×(\frac{3}{2})^{2026}$, 则 $a, b, c$ 的大小关系是 (D)
A. $b ＜ a ＜ c$
B. $a ＜ b ＜ c$
C. $a ＜ c ＜ b$
D. $c ＜ b ＜ a$

答案： D $a = 1$，$b = (2024 + 1)(2024 - 1) - 2024^{2} = 2024^{2} - 1 - 2024^{2} = -1$，$c = (-\frac{2}{3} \times \frac{3}{2})^{2025} \times \frac{3}{2} = -\frac{3}{2}$，
$\because -\frac{3}{2} ＜ -1 ＜ 1$，$\therefore c ＜ b ＜ a$.故选D.

10. 请利用平方差公式进行简便计算:
(1) $103×97$.
(2) $50\frac{1}{7}×49\frac{6}{7}$.

答案： 解析
(1)原式$= (100 + 3) \times (100 - 3) = 100^{2} - 3^{2} = 10000 - 9 = 9991$.
(2)原式$= (50 + \frac{1}{7}) \times (50 - \frac{1}{7}) = 50^{2} - (\frac{1}{7})^{2} = 2500 - \frac{1}{49} = 2499\frac{48}{49}$.

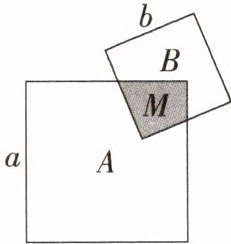
11. 如图,学校劳动实践基地有两块边长分别为 $a, b$ 的正方形秧田 $A, B$,其中不能使用的面积为 $M$.
(1) 用含 $a, M$ 的式子表示 $A$ 中能使用的面积:$a^{2} - M$.
(2) 若 $a + b = 10, a - b = 5$, 求 $A$ 比 $B$ 多出的使用面积.50

答案： 解析
(1)$a^{2} - M$.
(2)$\because a + b = 10$，$a - b = 5$，$\therefore (a + b)(a - b) = a^{2} - b^{2} = 10 \times 5 = 50$，$\therefore (a^{2} - M) - (b^{2} - M) = a^{2} - b^{2} = 50$.
故A比B多出的使用面积为50.