第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025山东烟台期末」下面是某同学对多项式$(x^{2}-4x)(x^{2}-4x+8)+16$进行因式分解的过程.
解:设$x^{2}-4x= m,$
则原式$=m(m+8)+16= m^{2}+8m+16= (m+4)^{2}$
$=(x^{2}-4x+4)^{2}= [(x-2)^{2}]^{2}= (x-2)^{4}.$
请根据上述材料将下列多项式进行因式分解:
(1)$(x^{2}-2x)(x^{2}-2x+2)+1.$
解:设$x^{2}-2x = n$,
则原式$=n(n + 2) + 1 = n^{2} + 2n + 1 = (n + 1)^{2}$
$=(x^{2}-2x + 1)^{2}= [(x - 1)^{2}]^{2}=$
(2)$(4a^{2}-12a+6)(4a^{2}-12a+12)+9.$
解:设$4a^{2}-12a = b$,
则原式$=(b + 6)(b + 12) + 9$
$=b^{2} + 18b + 72 + 9$
$=b^{2} + 18b + 81$
$=(b + 9)^{2}$
$=(4a^{2}-12a + 9)^{2}$
$=[(2a - 3)^{2}]^{2}=$
解:设$x^{2}-4x= m,$
则原式$=m(m+8)+16= m^{2}+8m+16= (m+4)^{2}$
$=(x^{2}-4x+4)^{2}= [(x-2)^{2}]^{2}= (x-2)^{4}.$
请根据上述材料将下列多项式进行因式分解:
(1)$(x^{2}-2x)(x^{2}-2x+2)+1.$
解:设$x^{2}-2x = n$,
则原式$=n(n + 2) + 1 = n^{2} + 2n + 1 = (n + 1)^{2}$
$=(x^{2}-2x + 1)^{2}= [(x - 1)^{2}]^{2}=$
$(x - 1)^{4}$
.(2)$(4a^{2}-12a+6)(4a^{2}-12a+12)+9.$
解:设$4a^{2}-12a = b$,
则原式$=(b + 6)(b + 12) + 9$
$=b^{2} + 18b + 72 + 9$
$=b^{2} + 18b + 81$
$=(b + 9)^{2}$
$=(4a^{2}-12a + 9)^{2}$
$=[(2a - 3)^{2}]^{2}=$
$(2a - 3)^{4}$
.
答案:
解析
(1) 设 $ x^{2}-2x = n $,
则 $ (x^{2}-2x)(x^{2}-2x + 2) + 1 $
$ = n(n + 2) + 1 = n^{2} + 2n + 1 = (n + 1)^{2} $
$ = (x^{2}-2x + 1)^{2} = [(x - 1)^{2}]^{2} = (x - 1)^{4} $。
(2) 设 $ 4a^{2}-12a = b $,
则 $ (4a^{2}-12a + 6)(4a^{2}-12a + 12) + 9 $
$ = (b + 6)(b + 12) + 9 $
$ = b^{2} + 18b + 72 + 9 $
$ = b^{2} + 18b + 81 $
$ = (b + 9)^{2} $
$ = (4a^{2}-12a + 9)^{2} $
$ = [(2a - 3)^{2}]^{2} $
$ = (2a - 3)^{4} $。
(1) 设 $ x^{2}-2x = n $,
则 $ (x^{2}-2x)(x^{2}-2x + 2) + 1 $
$ = n(n + 2) + 1 = n^{2} + 2n + 1 = (n + 1)^{2} $
$ = (x^{2}-2x + 1)^{2} = [(x - 1)^{2}]^{2} = (x - 1)^{4} $。
(2) 设 $ 4a^{2}-12a = b $,
则 $ (4a^{2}-12a + 6)(4a^{2}-12a + 12) + 9 $
$ = (b + 6)(b + 12) + 9 $
$ = b^{2} + 18b + 72 + 9 $
$ = b^{2} + 18b + 81 $
$ = (b + 9)^{2} $
$ = (4a^{2}-12a + 9)^{2} $
$ = [(2a - 3)^{2}]^{2} $
$ = (2a - 3)^{4} $。
2.「2025河南驻马店期中」阅读:用“十字相乘法”分解因式$2x^{2}-x-3$的方法.
二次项系数$2= 1×2.$
常数项$-3= -1×3= 1×(-3)$,验算:“交叉相乘之和”.
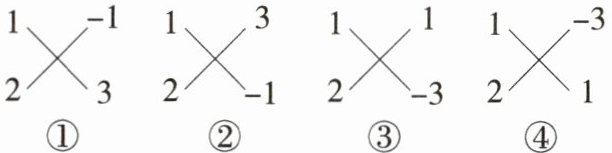
①$1×3+2×(-1)= 1$,②$1×(-1)+2×3= 5,$
③$1×(-3)+2×1= -1$,④$1×1+2×(-3)= -5.$
发现第③个“交叉相乘之和”的结果等于一次项系数-1,即$(x+1)(2x-3)= 2x^{2}-3x+2x-3= 2x^{2}-x-3$,则$2x^{2}-x-3= (x+1)(2x-3).$
像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫作十字相乘法.
仿照所给方法,分解因式:
(1)$x^{2}+8x+15=$
(2)$3x^{2}-5x-12=$
(3)$3(x+2)^{2}-5(x+2)-12=$
二次项系数$2= 1×2.$
常数项$-3= -1×3= 1×(-3)$,验算:“交叉相乘之和”.

①$1×3+2×(-1)= 1$,②$1×(-1)+2×3= 5,$
③$1×(-3)+2×1= -1$,④$1×1+2×(-3)= -5.$
发现第③个“交叉相乘之和”的结果等于一次项系数-1,即$(x+1)(2x-3)= 2x^{2}-3x+2x-3= 2x^{2}-x-3$,则$2x^{2}-x-3= (x+1)(2x-3).$
像这样,通过十字交叉线帮助,把二次三项式分解因式的方法,叫作十字相乘法.
仿照所给方法,分解因式:
(1)$x^{2}+8x+15=$
$(x + 3)(x + 5)$
.(2)$3x^{2}-5x-12=$
$(3x + 4)(x - 3)$
.(3)$3(x+2)^{2}-5(x+2)-12=$
$(3x + 10)(x - 1)$
.
答案:
解析
(1) $ x^{2} + 8x + 15 = (x + 3)(x + 5) $。
(2) $ 3x^{2}-5x - 12 = (3x + 4)(x - 3) $。
(3) $ 3(x + 2)^{2}-5(x + 2) - 12 $
$ = [3(x + 2) + 4][(x + 2) - 3] $
$ = (3x + 10)(x - 1) $。
(1) $ x^{2} + 8x + 15 = (x + 3)(x + 5) $。
(2) $ 3x^{2}-5x - 12 = (3x + 4)(x - 3) $。
(3) $ 3(x + 2)^{2}-5(x + 2) - 12 $
$ = [3(x + 2) + 4][(x + 2) - 3] $
$ = (3x + 10)(x - 1) $。
3.「2025江西南昌模拟」在对某些多项式进行因式分解时,需要把多项式中的某一项拆成两项或多项,或者在多项式中添上两个仅符号相反的项,这样分解因式的方法称为拆项添项法.如:
例1:分解因式:$x^{4}+4.$
解:原式$=x^{4}+4x^{2}+4-4x^{2}= (x^{2}+2)^{2}-4x^{2}$
$=(x^{2}-2x+2)(x^{2}+2x+2).$
例2:分解因式:$x^{3}+5x-6.$
解:原式$=x^{3}-x+6x-6$
$=x(x^{2}-1)+6(x-1)= (x-1)(x^{2}+x+6).$
请根据以上材料中的方法,解决下列问题:
(1)分解因式:$x^{2}+16x-36=$
(2)运用拆项添项法分解因式:
①$x^{4}+4y^{4}=$
②$x^{3}-x^{2}-4=$
例1:分解因式:$x^{4}+4.$
解:原式$=x^{4}+4x^{2}+4-4x^{2}= (x^{2}+2)^{2}-4x^{2}$
$=(x^{2}-2x+2)(x^{2}+2x+2).$
例2:分解因式:$x^{3}+5x-6.$
解:原式$=x^{3}-x+6x-6$
$=x(x^{2}-1)+6(x-1)= (x-1)(x^{2}+x+6).$
请根据以上材料中的方法,解决下列问题:
(1)分解因式:$x^{2}+16x-36=$
$(x + 18)(x - 2)$
.(2)运用拆项添项法分解因式:
①$x^{4}+4y^{4}=$
$(x^{2} + 2xy + 2y^{2})(x^{2}-2xy + 2y^{2})$
.②$x^{3}-x^{2}-4=$
$(x - 2)(x^{2} + x + 2)$
.
答案:
解析
(1) $ x^{2} + 16x - 36 $
$ = x^{2} + 16x + 64 - 64 - 36 $
$ = (x + 8)^{2}-100 $
$ = (x + 8 + 10)(x + 8 - 10) $
$ = (x + 18)(x - 2) $,
故答案为 $ (x + 18)(x - 2) $。
(2) ① $ x^{4} + 4y^{4} $
$ = x^{4} + 4x^{2}y^{2} + 4y^{4}-4x^{2}y^{2} $
$ = (x^{2} + 2y^{2})^{2}-4x^{2}y^{2} $
![img alt=3
(2)①]
$ = (x^{2} + 2xy + 2y^{2})(x^{2}-2xy + 2y^{2}) $。
② $ x^{3}-x^{2}-4 = x^{3}-2x^{2} + x^{2}-4 $
$ = x^{2}(x - 2) + (x + 2)(x - 2) $
$ = (x - 2)(x^{2} + x + 2) $。
(1) $ x^{2} + 16x - 36 $
$ = x^{2} + 16x + 64 - 64 - 36 $
$ = (x + 8)^{2}-100 $
$ = (x + 8 + 10)(x + 8 - 10) $
$ = (x + 18)(x - 2) $,
故答案为 $ (x + 18)(x - 2) $。
(2) ① $ x^{4} + 4y^{4} $
$ = x^{4} + 4x^{2}y^{2} + 4y^{4}-4x^{2}y^{2} $
$ = (x^{2} + 2y^{2})^{2}-4x^{2}y^{2} $
![img alt=3
(2)①]
$ = (x^{2} + 2xy + 2y^{2})(x^{2}-2xy + 2y^{2}) $。
② $ x^{3}-x^{2}-4 = x^{3}-2x^{2} + x^{2}-4 $
$ = x^{2}(x - 2) + (x + 2)(x - 2) $
$ = (x - 2)(x^{2} + x + 2) $。
查看更多完整答案,请扫码查看


