第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8.「2025山东潍坊期末改编,★☆」下列命题的逆命题是真命题的是(
A.全等三角形的面积相等
B.如果a= b,那么$a^2= b^2$
C.两直线平行,内错角相等
D.两个全等三角形的三对对应角相等
C
)A.全等三角形的面积相等
B.如果a= b,那么$a^2= b^2$
C.两直线平行,内错角相等
D.两个全等三角形的三对对应角相等
答案:
8.C 面积相等的三角形不一定全等,故A不符合题意;如果$a^{2}=b^{2}$,那么$a=\pm b$,故B不符合题意;内错角相等,两直线平行,故C符合题意;三角分别对应相等的三角形不一定全等,故D不符合题意。故选C。
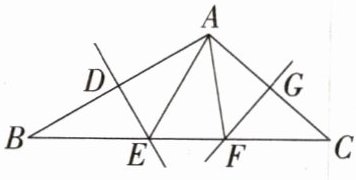
9.「2024湖北孝感期中,★☆」如图,在△ABC中,BC= 10,AB的垂直平分线交AB于点D,交BC于点E,AC的垂直平分线交AC于点G,交BC于点F,连接AE,AF,则△AEF的周长为______
10
.
答案:
答案 10
解析
∵DE是AB的垂直平分线,FG是AC的垂直平分线,
∴AE=BE,FA=FC,
∴△AEF的周长为AE+EF+AF=BE+EF+FC=BC=10。
解析
∵DE是AB的垂直平分线,FG是AC的垂直平分线,
∴AE=BE,FA=FC,
∴△AEF的周长为AE+EF+AF=BE+EF+FC=BC=10。
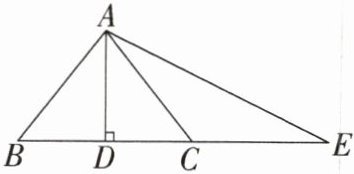
10.「★☆」如图,在△ABE中,AD⊥BE,C是DE上一点,且BD= CD,若C是AE垂直平分线上一点,AB= 5,AD= 4,BC= 6,则△ABE的面积为______
22
.
答案:
答案 22
解析
∵BD=CD,AD⊥BE,
∴AC=AB=5。
∵C是AE垂直平分线上一点,
∴CE=AC=5,
∴BE=BC+CE=6+5=11,
∴$S_{\triangle ABE}=\frac{1}{2}BE\cdot AD=\frac{1}{2}\times11\times4=22$。
解析
∵BD=CD,AD⊥BE,
∴AC=AB=5。
∵C是AE垂直平分线上一点,
∴CE=AC=5,
∴BE=BC+CE=6+5=11,
∴$S_{\triangle ABE}=\frac{1}{2}BE\cdot AD=\frac{1}{2}\times11\times4=22$。
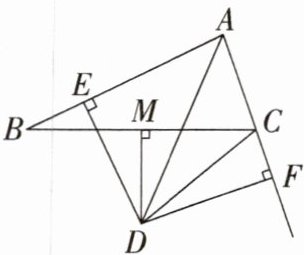
11.「2024山东烟台一中月考,★☆」如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并说明理由.

答案:
解析 AB=AE+CF。
理由:如图,连接DB,
∵点D在∠BAC的平分线上,DE⊥AB,DF⊥AC,
∴DE=DF。
∵点D在BC的垂直平分线上,
∴DB=DC。
在Rt△DBE与Rt△DCF中,$\begin{cases} DB=DC, \\ DE=DF, \end{cases}$
∴Rt△DBE≌Rt△DCF(HL),
∴BE=CF,
∴AB=AE+BE=AE+CF。

解析 AB=AE+CF。
理由:如图,连接DB,
∵点D在∠BAC的平分线上,DE⊥AB,DF⊥AC,
∴DE=DF。
∵点D在BC的垂直平分线上,
∴DB=DC。
在Rt△DBE与Rt△DCF中,$\begin{cases} DB=DC, \\ DE=DF, \end{cases}$
∴Rt△DBE≌Rt△DCF(HL),
∴BE=CF,
∴AB=AE+BE=AE+CF。

12.「2025湖南师大附中期末,★☆」如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD= DE,连接AE.
(1)求证:AB= EC.
(2)若△ABC的周长为32cm,AC= 12cm,求DC的长.
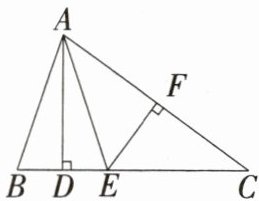
(1)证明:∵EF垂直平分AC,
∴AE=EC。
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC。
(2)由题意可得AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm。
∵AB=EC,BD=DE,
∴DC=DE+EC=$\frac{1}{2}BE+AB=\frac{1}{2}(BC-CE)+AB$=$\frac{1}{2}(BC-AB)+AB=\frac{1}{2}(AB+BC)=$
(1)求证:AB= EC.
(2)若△ABC的周长为32cm,AC= 12cm,求DC的长.

(1)证明:∵EF垂直平分AC,
∴AE=EC。
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC。
(2)由题意可得AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm。
∵AB=EC,BD=DE,
∴DC=DE+EC=$\frac{1}{2}BE+AB=\frac{1}{2}(BC-CE)+AB$=$\frac{1}{2}(BC-AB)+AB=\frac{1}{2}(AB+BC)=$
10
cm。
答案:
解析
(1)证明:
∵EF垂直平分AC,
∴AE=EC。
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC。
(2)由题意可得AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm。
∵AB=EC,BD=DE,
∴DC=DE+EC=$\frac{1}{2}BE+AB=\frac{1}{2}(BC-CE)+AB$=$\frac{1}{2}(BC-AB)+AB=\frac{1}{2}(AB+BC)=10$cm。
(1)证明:
∵EF垂直平分AC,
∴AE=EC。
∵AD⊥BC,BD=DE,
∴AD垂直平分BE,
∴AB=AE,
∴AB=EC。
(2)由题意可得AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm。
∵AB=EC,BD=DE,
∴DC=DE+EC=$\frac{1}{2}BE+AB=\frac{1}{2}(BC-CE)+AB$=$\frac{1}{2}(BC-AB)+AB=\frac{1}{2}(AB+BC)=10$cm。
13.「2025湖北荆门月考改编」如图,四边形ABCD中,∠A= ∠B= 90°,AB= 25cm,DA= 15cm,CB= 10cm.动点E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)求证:当x= 5时,点E在线段CD的垂直平分线上.
证明:当x=5时,AE=2×5=10(cm)=BC。
∵AB=25cm,DA=15cm,∴BE=15cm=AD。
在△ADE和△BEC中,$\begin{cases} AD=BE, \\ ∠A=∠B, \\ AE=BC, \end{cases}$
∴△ADE≌△BEC(SAS),∴DE=CE,
∴点E在线段CD的垂直平分线上。
故当x=5时,点E在线段CD的垂直平分线上。
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
理由如下:
∵△ADE≌△BEC,∴∠ADE=∠CEB。
∵∠A=90°,∴∠AED+∠ADE=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-90°=90°,∴DE⊥CE。
(1)求证:当x= 5时,点E在线段CD的垂直平分线上.
证明:当x=5时,AE=2×5=10(cm)=BC。
∵AB=25cm,DA=15cm,∴BE=15cm=AD。
在△ADE和△BEC中,$\begin{cases} AD=BE, \\ ∠A=∠B, \\ AE=BC, \end{cases}$
∴△ADE≌△BEC(SAS),∴DE=CE,
∴点E在线段CD的垂直平分线上。
故当x=5时,点E在线段CD的垂直平分线上。
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
DE⊥CE
理由如下:
∵△ADE≌△BEC,∴∠ADE=∠CEB。
∵∠A=90°,∴∠AED+∠ADE=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-90°=90°,∴DE⊥CE。
答案:
解析
(1)证明:当x=5时,AE=2×5=10(cm)=BC。
∵AB=25cm,DA=15cm,
∴BE=15cm=AD。
在△ADE和△BEC中,$\begin{cases} AD=BE, \\ ∠A=∠B, \\ AE=BC, \end{cases}$
∴△ADE≌△BEC(SAS),
∴DE=CE,
∴点E在线段CD的垂直平分线上。
故当x=5时,点E在线段CD的垂直平分线上。
(2)DE与CE的位置关系是DE⊥CE。理由如下:
∵△ADE≌△BEC,
∴∠ADE=∠CEB。
∵∠A=90°,
∴∠AED+∠ADE=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-90°=90°,
∴DE⊥CE。
(1)证明:当x=5时,AE=2×5=10(cm)=BC。
∵AB=25cm,DA=15cm,
∴BE=15cm=AD。
在△ADE和△BEC中,$\begin{cases} AD=BE, \\ ∠A=∠B, \\ AE=BC, \end{cases}$
∴△ADE≌△BEC(SAS),
∴DE=CE,
∴点E在线段CD的垂直平分线上。
故当x=5时,点E在线段CD的垂直平分线上。
(2)DE与CE的位置关系是DE⊥CE。理由如下:
∵△ADE≌△BEC,
∴∠ADE=∠CEB。
∵∠A=90°,
∴∠AED+∠ADE=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-90°=90°,
∴DE⊥CE。
查看更多完整答案,请扫码查看


