第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2024 湖北武汉中考」现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性。下列汉字是轴对称图形的是(

C
)
答案:
1.C 选项A、B、D中的汉字都不能找到一条直线,使图形沿这条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;选项C中的汉字能找到一条直线,使图形沿这条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.故选C.
2. 学习完轴对称图形知识后,小明在 $ 3 × 3 $ 的正方形网格中通过填充阴影来设计轴对称图形,其中是轴对称图形且有 $ 4 $ 条对称轴的是(
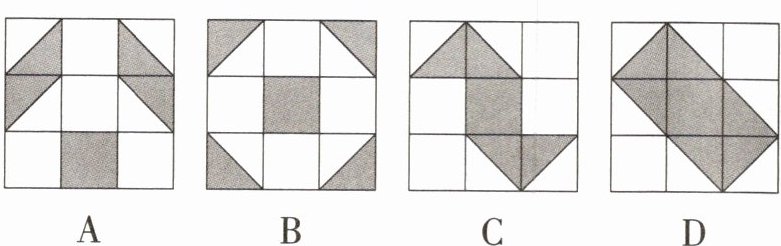
B
)
答案:
2.B A选项中的图案是轴对称图形,但只有1条对称轴,故本选项不符合题意;B选项中的图案是轴对称图形且有4条对称轴,故本选项符合题意;C选项中的图案不是轴对称图形,故本选项不符合题意;D选项中的图案是轴对称图形,但只有2条对称轴,故本选项不符合题意.故选B.
3. 新中华优秀传统文化「2025 陕西咸阳质检」二胡始于唐朝,是中国传统拉弦乐器。下列选项中左右两个二胡成轴对称的是(
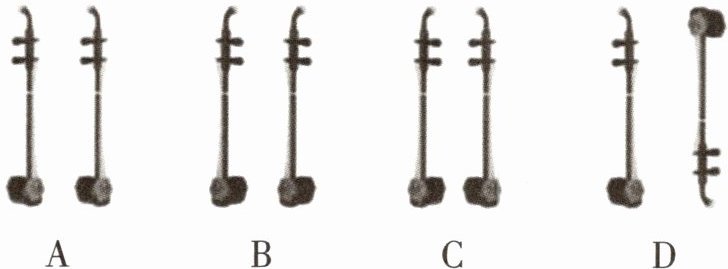
C
)
答案:
3.C A、B、D选项中的两个图形不能找到这样的一条直线,使其中一个图形沿这条直线折叠,能够与另一个图形互相重合,所以不成轴对称;C选项中的两个图形能找到这样的一条直线,使其中一个图形沿这条直线折叠,能够与另一个图形互相重合,所以成轴对称.故选C.
4.「2025 四川乐山月考」如图,$ \triangle ABC $ 与 $ \triangle DEF $ 关于直线 $ MN $ 对称,则以下结论中不一定正确的是(
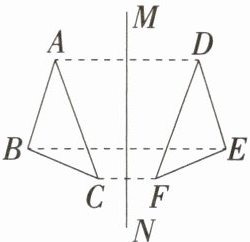
A. $ BC = DE $
B. $ \angle ABC = \angle DEF $
C. $ AD // BE $
D. $ AD $ 被 $ MN $ 垂直平分
A
)
A. $ BC = DE $
B. $ \angle ABC = \angle DEF $
C. $ AD // BE $
D. $ AD $ 被 $ MN $ 垂直平分
答案:
4.A
∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∴BC=EF,∠ABC=∠DEF,故选项A不一定正确,选项B正确;
∵△ABC与△DEF关于直线MN对称,
∴AD⊥MN,BE⊥MN,
∴AD//BE,AD被MN垂直平分,故选项C、D正确.故选A.
∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∴BC=EF,∠ABC=∠DEF,故选项A不一定正确,选项B正确;
∵△ABC与△DEF关于直线MN对称,
∴AD⊥MN,BE⊥MN,
∴AD//BE,AD被MN垂直平分,故选项C、D正确.故选A.
5.《周髀算经》中提出了“方属地,圆属天”,就是人们常说的“天圆地方”。我国古代铜钱的铸造也蕴含了这种“外圆内方”“天地合一”的哲学思想,现将铜钱抽象成如图所示的图形,$ AC $,$ BD $ 为圆 $ O $ 的直径,$ AC \perp BD $,若圆 $ O $ 的面积为 $ 16 \pi \text{ cm}^2 $,则图中阴影部分的面积为______
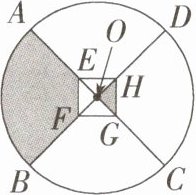
4π
$ \text{cm}^2 $。
答案:
5.答案 4π
解析
∵AC,BD为圆O的直径,AC⊥BD,
∴S_{△OEF}=S_{△OFG}=S_{△OGH}=S_{△OEH},
∴S_{阴影}=S_{扇形AOB}=$\frac{1}{4}$S_{圆},
∵圆O的面积为16π cm²,
∴S_{阴影}=4π cm².
解析
∵AC,BD为圆O的直径,AC⊥BD,
∴S_{△OEF}=S_{△OFG}=S_{△OGH}=S_{△OEH},
∴S_{阴影}=S_{扇形AOB}=$\frac{1}{4}$S_{圆},
∵圆O的面积为16π cm²,
∴S_{阴影}=4π cm².
6.「★☆」小强从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是(

A. $ 15:01 $
B. $ 10:51 $
C. $ 10:21 $
D. $ 12:01 $
C
)
A. $ 15:01 $
B. $ 10:51 $
C. $ 10:21 $
D. $ 12:01 $
答案:
6.C 根据镜面对称可知电子表的实际时刻是10:21.故选C.
7.「2025 山东聊城期末,★☆」如图,在 $ \triangle ABC $ 中,$ \angle B = 50^\circ $,$ \angle C = 80^\circ $,点 $ D $ 是 $ BC $ 上任意一点,点 $ M $ 和点 $ N $ 分别是点 $ D $ 关于 $ AB $ 和 $ AC $ 的对称点,连接 $ AM $ 和 $ AN $,则 $ \angle MAN $ 的度数为______。
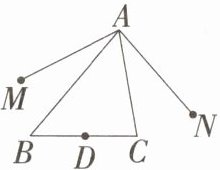

答案:
7.答案 100°
解析 如图,连接AD,
∵点M和点N分别是点D关于AB和AC的对称点,

∴∠MAB=∠BAD,∠NAC=∠CAD,
∵∠B=50°,∠C=80°,
∴∠BAC=∠BAD+∠DAC=180°−80°−50°=50°,
∴∠MAN=2∠BAC=100°.
7.答案 100°
解析 如图,连接AD,
∵点M和点N分别是点D关于AB和AC的对称点,

∴∠MAB=∠BAD,∠NAC=∠CAD,
∵∠B=50°,∠C=80°,
∴∠BAC=∠BAD+∠DAC=180°−80°−50°=50°,
∴∠MAN=2∠BAC=100°.
8.「2025 浙江衢州质检,★☆」如图,$ \triangle ABC $ 和 $ \triangle ADE $ 关于直线 $ MN $ 对称,$ BC $ 和 $ DE $ 的交点 $ F $ 在直线 $ MN $ 上。
(1) 若 $ ED = 15 $,$ BF = 9 $,求 $ EF $ 的长。
(2) 若 $ \angle ABC = 35^\circ $,$ \angle AED = 65^\circ $,$ \angle BAE = 16^\circ $,求 $ \angle BFN $ 的度数。
(3) 连接 $ BD $ 和 $ EC $,判断 $ BD $ 和 $ EC $ 的位置关系,并说明理由。
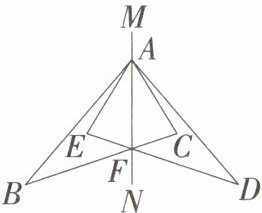
(1) 若 $ ED = 15 $,$ BF = 9 $,求 $ EF $ 的长。
(2) 若 $ \angle ABC = 35^\circ $,$ \angle AED = 65^\circ $,$ \angle BAE = 16^\circ $,求 $ \angle BFN $ 的度数。
(3) 连接 $ BD $ 和 $ EC $,判断 $ BD $ 和 $ EC $ 的位置关系,并说明理由。

答案:
8.解析
(1)
∵△ABC和△ADE关于直线MN对称,BF=9,
∴DF=BF=9,
又
∵ED=15,
∴EF=ED−DF=15−9=6.
(2)
∵△ABC和△ADE关于直线MN对称,∠AED=65°,
∴∠ACB=∠AED=65°,
∴∠BAC=180°−∠ABC−∠ACB=180°−35°−65°=80°,
∵∠BAE=16°,
∴∠EAC=∠BAC−∠BAE=80°−16°=64°,
∵线段AE与AC关于直线MN对称,
∴∠EAN=∠CAN=$\frac{1}{2}$∠EAC=$\frac{1}{2}$×64°=32°,
∴∠BAN=∠BAE+∠EAN=16°+32°=48°,
∴∠BFN=∠ABC+∠BAN=35°+48°=83°.
(3)BD//EC.理由:如图,

易得MN⊥EC,MN⊥BD,
∴BD//EC.
8.解析
(1)
∵△ABC和△ADE关于直线MN对称,BF=9,
∴DF=BF=9,
又
∵ED=15,
∴EF=ED−DF=15−9=6.
(2)
∵△ABC和△ADE关于直线MN对称,∠AED=65°,
∴∠ACB=∠AED=65°,
∴∠BAC=180°−∠ABC−∠ACB=180°−35°−65°=80°,
∵∠BAE=16°,
∴∠EAC=∠BAC−∠BAE=80°−16°=64°,
∵线段AE与AC关于直线MN对称,
∴∠EAN=∠CAN=$\frac{1}{2}$∠EAC=$\frac{1}{2}$×64°=32°,
∴∠BAN=∠BAE+∠EAN=16°+32°=48°,
∴∠BFN=∠ABC+∠BAN=35°+48°=83°.
(3)BD//EC.理由:如图,

易得MN⊥EC,MN⊥BD,
∴BD//EC.
查看更多完整答案,请扫码查看


