第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 在探究证明“三角形的内角和是$180^{\circ }$”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是$180^{\circ }$”的是(

C
)
答案:
1.C 列表分析如下:
|选项|分析|是否符合题意|
|----|----|----|
|A|$\left.\begin{array}{l}EF// AB\to \angle ECA=\angle A,\\ \angle FCB=\angle B\\ \angle ECA+\angle ACB+\angle FCB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle A+\angle ACB+\angle B={180}^{\circ }$|否|
|续表|
|选项|分析|是否符合题意|
|B|$\left.\begin{array}{l}CE// AB\to \angle A=\angle FCE,\\ \angle B=\angle BCE\\ \angle FCE+\angle ECB+\angle ACB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle A+\angle B+\angle ACB={180}^{\circ }$|否|
|C|$CD\perp AB\to \angle ADC=\angle CDB={90}^{\circ }$|是|
|D|$\left.\begin{array}{l}DF// AC\to \angle EDF=\\ \angle AED,\angle A=\angle FDB\\ ED// CB\to \angle EDA=\\ \angle B,\angle C=\angle AED\\ \angle ADE+\angle EDF+\angle FDB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle B+\angle C+\angle A={180}^{\circ }$|否|
故选C.
|选项|分析|是否符合题意|
|----|----|----|
|A|$\left.\begin{array}{l}EF// AB\to \angle ECA=\angle A,\\ \angle FCB=\angle B\\ \angle ECA+\angle ACB+\angle FCB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle A+\angle ACB+\angle B={180}^{\circ }$|否|
|续表|
|选项|分析|是否符合题意|
|B|$\left.\begin{array}{l}CE// AB\to \angle A=\angle FCE,\\ \angle B=\angle BCE\\ \angle FCE+\angle ECB+\angle ACB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle A+\angle B+\angle ACB={180}^{\circ }$|否|
|C|$CD\perp AB\to \angle ADC=\angle CDB={90}^{\circ }$|是|
|D|$\left.\begin{array}{l}DF// AC\to \angle EDF=\\ \angle AED,\angle A=\angle FDB\\ ED// CB\to \angle EDA=\\ \angle B,\angle C=\angle AED\\ \angle ADE+\angle EDF+\angle FDB\\ ={180}^{\circ }\end{array}\right\}\Rightarrow \angle B+\angle C+\angle A={180}^{\circ }$|否|
故选C.
2. 在$△ABC$中,$∠A:∠B:∠C= 1:3:4$,则$△ABC$中最大的内角度数为(
A.$80^{\circ }$
B.$90^{\circ }$
C.$100^{\circ }$
D.$120^{\circ }$
B
)A.$80^{\circ }$
B.$90^{\circ }$
C.$100^{\circ }$
D.$120^{\circ }$
答案:
2.B
∵在△ABC中,∠A:∠B:∠C = 1:3:4,
∴设∠A = x,则∠B = 3x,∠C = 4x,
∴x + 3x + 4x = 180°,解得x = 22.5°,
∴∠C = 4x = 4×22.5° = 90°,
故选B.
归纳总结 题目中出现角度的比例关系时,常设单份比例为x,用含x的式子表示各个角的度数,然后根据三角形内角和定理列方程求解。
∵在△ABC中,∠A:∠B:∠C = 1:3:4,
∴设∠A = x,则∠B = 3x,∠C = 4x,
∴x + 3x + 4x = 180°,解得x = 22.5°,
∴∠C = 4x = 4×22.5° = 90°,
故选B.
归纳总结 题目中出现角度的比例关系时,常设单份比例为x,用含x的式子表示各个角的度数,然后根据三角形内角和定理列方程求解。
3. 如图,点E,D分别在AB,AC上,若$∠B= 30^{\circ },∠C= 55^{\circ }$,则$∠1+∠2$的度数为(

A.$85^{\circ }$
B.$80^{\circ }$
C.$75^{\circ }$
D.$70^{\circ }$
A
)
A.$85^{\circ }$
B.$80^{\circ }$
C.$75^{\circ }$
D.$70^{\circ }$
答案:
3.A [解法一]在△ABC中,∠A = 180°−∠B−∠C = 95°。在△AED中,∠1 + ∠2 = 180°−∠A = 85°。
[解法二]
∵∠1 + ∠2 + ∠A = 180°,∠B + ∠C + ∠A = 180°,
∴∠1 + ∠2 = ∠B + ∠C,
∵∠B = 30°,∠C = 55°,
∴∠1 + ∠2 = ∠B + ∠C = 30° + 55° = 85°。
故选A.
[解法二]
∵∠1 + ∠2 + ∠A = 180°,∠B + ∠C + ∠A = 180°,
∴∠1 + ∠2 = ∠B + ∠C,
∵∠B = 30°,∠C = 55°,
∴∠1 + ∠2 = ∠B + ∠C = 30° + 55° = 85°。
故选A.
4. 如图,△ABC缺了一个角,测得$∠A= 70^{\circ },∠B=24^{\circ },$则∠C的度数是(
A.$84^{\circ }$
B.$86^{\circ }$
C.$96^{\circ }$
D.$66^{\circ }$
B
)A.$84^{\circ }$
B.$86^{\circ }$
C.$96^{\circ }$
D.$66^{\circ }$
答案:
4.B
∵∠A + ∠B + ∠C = 180°,∠A = 70°,∠B = 24°,
∴∠C = 180°−70°−24° = 86°,
故选B.
∵∠A + ∠B + ∠C = 180°,∠A = 70°,∠B = 24°,
∴∠C = 180°−70°−24° = 86°,
故选B.
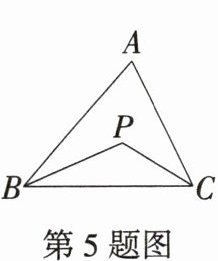
5. 如图,$∠A= 70^{\circ },BP,CP分别平分∠ABC和∠ACB$,则$∠P$的度数是______
125°
.
答案:
5.答案 125°
解析 在△ABC中,∠A = 70°,
∴∠ABC + ∠ACB = 180°−∠A = 180°−70° = 110°。
∵BP,CP分别平分∠ABC和∠ACB,
∴∠PBC = $\frac{1}{2}$∠ABC,∠PCB = $\frac{1}{2}$∠ACB。在△PBC中,∠P + ∠PBC + ∠PCB = 180°,
∴∠P = 180°−(∠PBC + ∠PCB)=180°−$\frac{1}{2}$(∠ABC + ∠ACB)=180°−$\frac{1}{2}$×110° = 125°。
解析 在△ABC中,∠A = 70°,
∴∠ABC + ∠ACB = 180°−∠A = 180°−70° = 110°。
∵BP,CP分别平分∠ABC和∠ACB,
∴∠PBC = $\frac{1}{2}$∠ABC,∠PCB = $\frac{1}{2}$∠ACB。在△PBC中,∠P + ∠PBC + ∠PCB = 180°,
∴∠P = 180°−(∠PBC + ∠PCB)=180°−$\frac{1}{2}$(∠ABC + ∠ACB)=180°−$\frac{1}{2}$×110° = 125°。
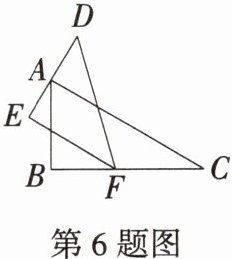
6. 一副三角尺按如图所示的方式放置,点A在DE上,点F在BC上,若$∠EAB= 35^{\circ }$,则$∠DFC= $______.

答案:
6.答案 100°
解析 如图,设AC与DF交于点G,
由题意得∠BAC = 60°,∠C = 30°,∠D = 45°,
∵∠EAB = 35°,
∴∠CAD = 180°−∠EAB−∠BAC = 85°,
∴∠AGD = 180°−∠D−∠CAD = 50°,
∴∠CGF = ∠AGD = 50°,
∴∠DFC = 180°−∠C−∠CGF = 100°。

6.答案 100°
解析 如图,设AC与DF交于点G,
由题意得∠BAC = 60°,∠C = 30°,∠D = 45°,
∵∠EAB = 35°,
∴∠CAD = 180°−∠EAB−∠BAC = 85°,
∴∠AGD = 180°−∠D−∠CAD = 50°,
∴∠CGF = ∠AGD = 50°,
∴∠DFC = 180°−∠C−∠CGF = 100°。

7. 如图,在$△ABC$中,$∠A= 46^{\circ }$,CE是$∠ACB$的平分线,交AB于点E,点B,C,D在同一条直线上,$FD// EC$交AB于点F,$∠D= 42^{\circ }$,求$∠B$的度数.


50°
答案:
7.解析
∵FD//EC,∠D = 42°,
∴∠BCE = ∠D = 42°,
∵CE是∠ACB的平分线,
∴∠ACB = 2∠BCE = 84°,
∵∠A = 46°,
∴∠B = 180°−84°−46° = 50°。
∵FD//EC,∠D = 42°,
∴∠BCE = ∠D = 42°,
∵CE是∠ACB的平分线,
∴∠ACB = 2∠BCE = 84°,
∵∠A = 46°,
∴∠B = 180°−84°−46° = 50°。
8. 如图,轮船在B处观测灯塔A位于南偏东$75^{\circ }$方向上,轮船从B处以每小时50海里的速度沿南偏东$30^{\circ }$方向匀速航行,半小时到达C处,在C处观测灯塔A位于北偏东$60^{\circ }$方向上,求$∠A$的度数.


答案:
8.解析 如图,根据题意知∠1 = ∠2 = 30°,
∴∠CBA = 75°−30° = 45°,
∵∠ACD = 60°,
∴∠ACB = 30° + 60° = 90°,
∴∠A = 180°−90°−45° = 45°。

8.解析 如图,根据题意知∠1 = ∠2 = 30°,
∴∠CBA = 75°−30° = 45°,
∵∠ACD = 60°,
∴∠ACB = 30° + 60° = 90°,
∴∠A = 180°−90°−45° = 45°。

9. 如图,在$△ABC$中,$∠A= 70^{\circ },∠C= 30^{\circ }$,BD平分$∠ABC$交AC于点D,$DE// AB$,交BC于点E,则$∠BDE$的度数是(

A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
B
)
A.$30^{\circ }$
B.$40^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
答案:
9.B 在△ABC中,∠A = 70°,∠C = 30°,
∴∠ABC = 180°−∠A−∠C = 80°,
∵BD平分∠ABC,
∴∠ABD = $\frac{1}{2}$∠ABC = 40°,
∵DE//AB,
∴∠BDE = ∠ABD = 40°,故选B.
∴∠ABC = 180°−∠A−∠C = 80°,
∵BD平分∠ABC,
∴∠ABD = $\frac{1}{2}$∠ABC = 40°,
∵DE//AB,
∴∠BDE = ∠ABD = 40°,故选B.
查看更多完整答案,请扫码查看


