《2025年5年中考3年模拟八年级数学上册人教版》

1.新操作实践题 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到 (C)

A.三角形
B.梯形
C.正方形
D.五边形

答案： C

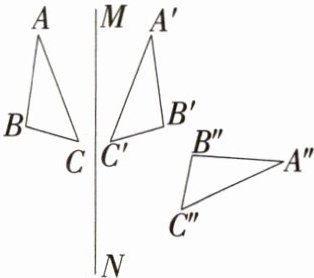
2.如图,$△ABC和△A'B'C'$关于直线MN对称,$△A'B'C'和△A''B''C''$关于直线EF对称.
(1)作出直线EF.
(2)直线MN,EF相交于点O,试探究$∠BOB''$与直线MN,EF所夹锐角α的数量关系.

答案：
解析
(1) 如图，连接 $ B'B'' $，作线段 $ B'B'' $ 的垂直平分线 $ EF $，则直线 $ EF $ 是 $ \triangle A'B'C' $ 和 $ \triangle A''B''C'' $ 的对称轴。

(2) 如图，连接 $ BO $，$ B'O $，$ B''O $。
$ \because \triangle ABC $ 和 $ \triangle A'B'C' $ 关于直线 $ MN $ 对称，
$ \therefore \angle BOM = \angle B'OM $。
$ \because \triangle A'B'C' $ 和 $ \triangle A''B''C'' $ 关于直线 $ EF $ 对称，
$ \therefore \angle B'OE = \angle B''OE $。
$ \therefore \angle BOB'' = \angle BOM + \angle B'OM + \angle B'OE + \angle B''OE = 2(\angle B'OM + \angle B'OE) = 2\alpha $。

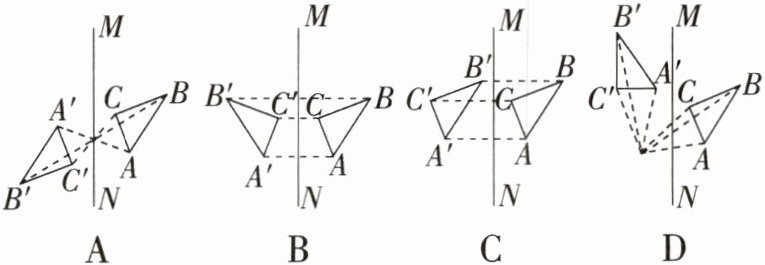
3.学科教材特色变式 下面是四位同学作$△ABC$关于直线MN对称的图形,其中正确的是 (B)

答案： B

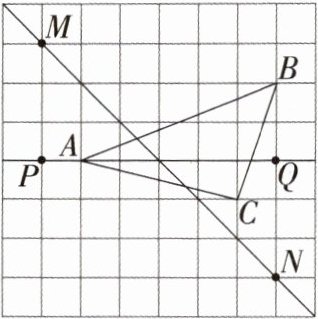
4.如图,在$8×8的正方形网格中有一个△ABC$,点A、B、C、M、N、P、Q都在格点上,分别画出$△ABC$关于直线PQ对称的$△A_{1}B_{1}C_{1}$和关于直线MN对称的$△A_{2}B_{2}C_{2}$.

答案：
解析 如图，$ \triangle A_1B_1C_1 $ 即为 $ \triangle ABC $ 关于直线 $ PQ $ 对称的图形，$ \triangle A_2B_2C_2 $ 即为 $ \triangle ABC $ 关于直线 $ MN $ 对称的图形。

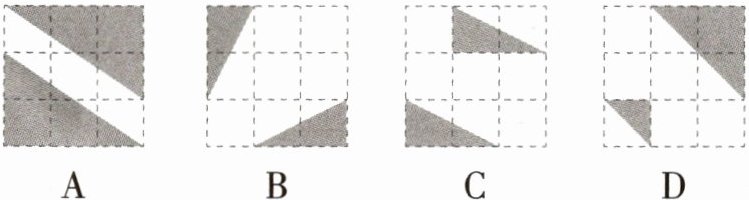
5.「2024湖北武汉模拟,★☆」下列每个网格中均有两个图形,其中一个图形可以由另一个进行轴对称变换得到的是 (B)

答案： B 根据轴对称的定义可知，选项 B 中一个图形可以由另一个进行轴对称变换得到。故选 B。

6.「2025山东泰安月考,★☆」作图题:如图所示的是由9个相同的小正方形拼成的正方形网格,现将其中2个小正方形涂灰,请用3种不同的方法分别在图中再将2个小正方形涂灰,使图案成为轴对称图形.

答案：
解析 答案不唯一，如图所示。

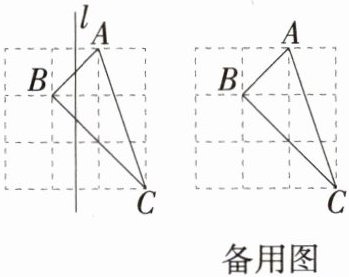
7.「2025上海静安期末,★☆」如图所示的是$3×3$的正方形网格,图中三角形ABC为格点三角形.
(1)在图中画出三角形ABC关于直线l成轴对称的三角形.
(2)在该网格中是否还存在与三角形ABC成轴对称的其他格点三角形? 如果存在,请在备用图中画出该三角形,并画出相应的对称轴.

答案：
解析
(1) 如图，$ \triangle A'B'C' $ 即为所求作。

(2) 如图，$ \triangle AB''C'' $ 和直线 $ l $ 即为所求作（答案不唯一）。