《2025年5年中考3年模拟八年级数学上册人教版》

11.图①是一台可折叠的床头伸缩壁灯,图②是其示意图.已知调整前、后的灯杆$AB// CD$,调整前臂杆之间的夹角$∠OAB= 75^{\circ }$,调整后臂杆之间的夹角$∠OCD= 100^{\circ }$,则调整前、后同一臂杆变化的角度$∠AOC= $______$^{\circ }$.

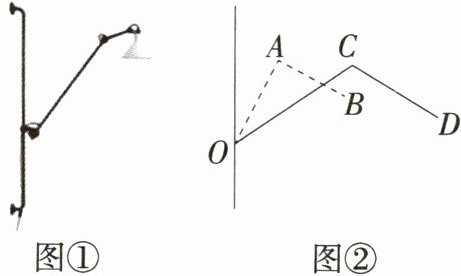
答案：
答案 $ 25 $
解析 如图，$ \because AB // CD $，$ \therefore \angle C = \angle \alpha = 100^\circ $，$ \because \angle \alpha = \angle AOC + \angle OAB $，$ \therefore \angle AOC = \angle \alpha - \angle OAB = 100^\circ - 75^\circ = 25^\circ $。故答案为 $ 25 $。

12.「2025 河北唐山九中月考」如图,AD是$\triangle ABC$的角平分线,CE 是$\triangle ABC$的高,$∠BAC= 60^{\circ },$$∠BCE= 50^{\circ }$,点 F 为边 AB 上一点,当$\triangle BDF$为直角三角形时,$∠ADF$的度数为______.

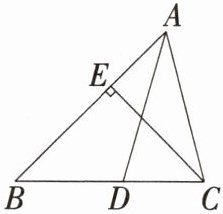
答案：
答案 $ 20^\circ $ 或 $ 60^\circ $
解析 如图所示，当 $ \angle BFD = 90^\circ $ 时，

$ \because AD $ 是 $ \triangle ABC $ 的角平分线，$ \angle BAC = 60^\circ $，$ \therefore \angle BAD = 30^\circ $，$ \therefore \text{Rt}\triangle ADF $ 中，$ \angle ADF = 60^\circ $；
如图，当 $ \angle BDF = 90^\circ $ 时，

同理可得 $ \angle BAD = 30^\circ $，$ \because CE $ 是 $ \triangle ABC $ 的高，$ \angle BCE = 50^\circ $，$ \therefore \angle BFD = \angle BCE = 50^\circ $，$ \therefore \angle ADF = \angle BFD - \angle BAD = 20^\circ $。
综上所述，$ \angle ADF $ 的度数为 $ 20^\circ $ 或 $ 60^\circ $。

13.学科特色分类讨论思想「2025 山东德州期中」(8 分)在$\triangle ABC$中,已知$AB= 14,BC= 8,AC= 2m-2.$
(1)求 m 的取值范围.$4 ＜ m ＜ 12$
(2)若$\triangle ABC$是等腰三角形,求$\triangle ABC$的周长.36 或 30

答案： 解析 （1）在 $ \triangle ABC $ 中，$ AB = 14 $，$ BC = 8 $，$ AC = 2m - 2 $，$ \therefore 14 - 8 ＜ 2m - 2 ＜ 14 + 8 $，解得 $ 4 ＜ m ＜ 12 $，$ \therefore m $ 的取值范围为 $ 4 ＜ m ＜ 12 $。
（2）$ \because \triangle ABC $ 是等腰三角形，$ \therefore $ 分两种情况：
① 当 $ AB = AC = 14 $ 时，$ 2m - 2 = 14 $，$ \therefore m = 8 $，$ \therefore \triangle ABC $ 的周长 $ = 14 + 14 + 8 = 36 $；
② 当 $ BC = AC = 8 $ 时，$ 2m - 2 = 8 $，$ \therefore m = 5 $，$ \therefore \triangle ABC $ 的周长 $ = 8 + 14 + 8 = 30 $。
综上所述，$ \triangle ABC $ 的周长为 $ 36 $ 或 $ 30 $。

14.(8 分)如图,在$\triangle ABC$中,$∠B+∠C= 90^{\circ }$,AD 是$\triangle ABC$的中线,AE 是$\triangle ABC$的高,F 为 AD 上一点,过点 F 作$FG⊥BC$于点 G,且$AE= 4FG.$
(1)求证:$\triangle ABC$是直角三角形.
(2)若$∠B= ∠BAD,∠C= 60^{\circ }$,求$∠DFG$的度数.30°
(3)若$DC= 5,FG= \frac {6}{5}$,求$\triangle ABC$的面积.24

答案： 解析 （1）证明：$ \because \angle B + \angle C = 90^\circ $，$ \therefore \angle BAC = 180^\circ - (\angle B + \angle C) = 90^\circ $，$ \therefore \triangle ABC $ 是直角三角形。
（2）$ \because \angle C = 60^\circ $，$ \angle BAC = 90^\circ $，$ \therefore \angle B = \angle BAD = 30^\circ $，$ \therefore \angle ADC = \angle B + \angle BAD = 60^\circ $，$ \because FG \perp BC $，$ \therefore \angle FGD = 90^\circ $，$ \therefore \angle DFG = 30^\circ $。
（3）$ \because AE $ 是 $ \triangle ABC $ 的高，$ \therefore \angle AEC = 90^\circ $，$ \because AE = 4FG $，$ FG = \frac{6}{5} $，$ \therefore AE = \frac{24}{5} $，$ \because AD $ 是 $ \triangle ABC $ 的中线，$ DC = 5 $，$ \therefore BC = 10 $，$ \therefore S_{\triangle ABC} = \frac{1}{2}BC \cdot AE = \frac{1}{2} \times 10 \times \frac{24}{5} = 24 $。

15.(12 分)如图,在$\triangle ABC$中,P 是线段 BC 上的一个动点,且不与 B,C 重合,$PD⊥AB,PE⊥AC.$
(1)如图 1,已知$∠BAC= 80^{\circ },∠B= ∠C.$
①$∠DPE= $100$^{\circ }$.
②若$∠APB= 3∠PAC$,则$∠APD= $35$^{\circ }$.
(2)如图 2,已知$AB= AC$,作$BF⊥AC$于 F,试探究 BF,PE,PD 之间的关系.BF=PE+PD

答案： 解析 （1）① 在四边形 $ AEPD $ 中，$ \angle DPE = 360^\circ - \angle BAC - \angle ADP - \angle AEP = 360^\circ - 80^\circ - 90^\circ - 90^\circ = 100^\circ $。
② $ \because \angle BAC = 80^\circ $，$ \angle B = \angle C $，$ \therefore \angle B = \angle C = \frac{1}{2}(180^\circ - \angle BAC) = \frac{1}{2} \times (180^\circ - 80^\circ) = 50^\circ $，则 $ \angle DPB = 90^\circ - \angle B = 40^\circ $，设 $ \angle PAC = \alpha $，则 $ \angle APB = 3\angle PAC = 3\alpha $，$ \angle APE = 90^\circ - \angle PAE = 90^\circ - \alpha $，则 $ \angle APD = \angle APB - \angle DPB = 3\alpha - 40^\circ $，则 $ \angle DPE = 100^\circ = \angle APD + \angle APE = 3\alpha - 40^\circ + 90^\circ - \alpha $，解得 $ \alpha = 25^\circ $，则 $ \angle APD = 3\alpha - 40^\circ = 35^\circ $。
（2）$ \because S_{\triangle ABC} = S_{\triangle ABP} + S_{\triangle ACP} $，$ \therefore \frac{1}{2}BF \cdot AC = \frac{1}{2}AB \cdot PD + \frac{1}{2}AC \cdot PE $，$ \because AB = AC $，$ \therefore BF = PE + PD $。

16.「2025 河南平顶山期末」(12 分)如图,点 C,D 分别在射线 OA,OB 上,CE 是$∠ACD$的平分线,CE 的反向延长线与$∠ODC$的平分线交于点 P.
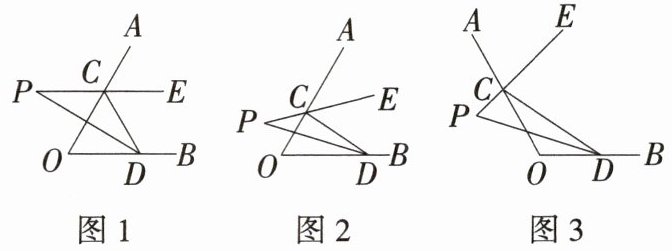
(1)如图 1,当$∠AOB= ∠OCD= 60^{\circ }$时,$∠P= $______30$^{\circ }$.
(2)如图 2,当$∠AOB= 60^{\circ }$,点 C,D 在射线OA,OB 上任意移动时(不与点 O 重合),$∠P$的大小是否变化? 若变化,请说明理由;若不变,请求出$∠P$的度数.
(3)如图 3,若$∠OCD+∠ODC= α(0^{\circ }＜α＜$$180^{\circ })$,请直接写出$∠P$的度数(用含α的式子表示).$90^{\circ }-\frac {1}{2}α$

答案： 解析 （1）$ \because \angle AOB = \angle OCD = 60^\circ $，$ \therefore \angle ACD = 180^\circ - \angle OCD = 180^\circ - 60^\circ = 120^\circ $，$ \angle ODC = 180^\circ - \angle AOB - \angle OCD = 60^\circ $，$ \because CE $ 平分 $ \angle ACD $，$ DP $ 平分 $ \angle ODC $，$ \therefore \angle ECD = \frac{1}{2}\angle ACD = \frac{1}{2} \times 120^\circ = 60^\circ $，$ \angle PDC = \frac{1}{2}\angle ODC = \frac{1}{2} \times 60^\circ = 30^\circ $，$ \because \angle ECD = \angle P + \angle PDC $，$ \therefore \angle P = \angle ECD - \angle PDC = 60^\circ - 30^\circ = 30^\circ $，故答案为 $ 30 $。
（2）$ \angle P $ 的大小不变。$ \because CE $ 平分 $ \angle ACD $，$ DP $ 平分 $ \angle ODC $，$ \therefore \angle ECD = \frac{1}{2}\angle ACD $，$ \angle PDC = \frac{1}{2}\angle ODC $，$ \therefore \frac{1}{2}\angle ACD = \angle P + \frac{1}{2}\angle ODC $，又 $ \because \frac{1}{2}\angle ACD = \frac{1}{2}(\angle AOB + \angle ODC) $，$ \therefore \angle P = \frac{1}{2}\angle AOB = \frac{1}{2} \times 60^\circ = 30^\circ $。
（3）$ \angle P = 90^\circ - \frac{1}{2}\alpha $。
详解：$ \because \angle OCD + \angle ODC = \alpha $，$ \therefore \angle AOB = 180^\circ - (\angle OCD + \angle ODC) = 180^\circ - \alpha $，由（2）可得 $ \angle P = \frac{1}{2}\angle AOB = \frac{1}{2}(180^\circ - \alpha) = 90^\circ - \frac{1}{2}\alpha $。