第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 下列选项中,$∠1为△ABC$的外角的是(
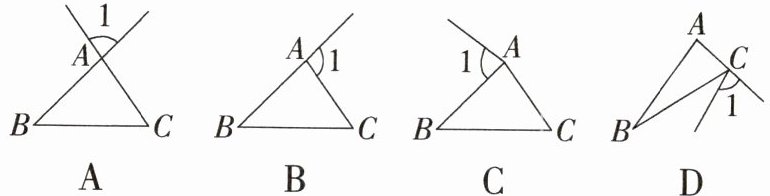
B
)
答案:
B 只有 B 选项中的∠1是△ABC的外角. 故选 B.
2. 学科教材 特色变式 [2025 广东珠海期中] 如图,$∠A = 40^{\circ}$,$∠CBD是△ABC$的外角,$∠C = 60^{\circ}$,则$∠CBD$的大小是(

A. $180^{\circ}$
B. $120^{\circ}$
C. $100^{\circ}$
D. $80^{\circ}$
C
)
A. $180^{\circ}$
B. $120^{\circ}$
C. $100^{\circ}$
D. $80^{\circ}$
答案:
C
∵∠A = 40°,∠C = 60°,∠CBD是△ABC的外角,
∴∠CBD = ∠A + ∠C = 100°. 故选 C.
∵∠A = 40°,∠C = 60°,∠CBD是△ABC的外角,
∴∠CBD = ∠A + ∠C = 100°. 故选 C.
3. 如图,下列说法中错误的是(
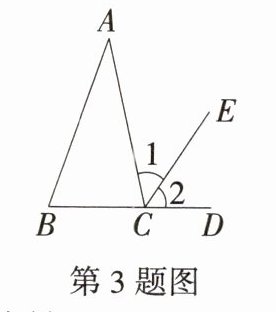
A. $∠1不是三角形ABC$的外角
B. $∠ACD是三角形ABC$的外角
C. $∠ACD > ∠A + ∠B$
D. $∠B < ∠1 + ∠2$
C
)
A. $∠1不是三角形ABC$的外角
B. $∠ACD是三角形ABC$的外角
C. $∠ACD > ∠A + ∠B$
D. $∠B < ∠1 + ∠2$
答案:
C A.∠1不是三角形ABC的外角,正确;B.∠ACD是三角形ABC的外角,正确;C.∠ACD = ∠A + ∠B,原说法错误;D.∠B < ∠1 + ∠2,正确. 故选 C.
4. [2025 浙江杭州期中] 将一副三角尺按照如图所示的方式摆放,点$C$、$B$、$E$共线,$∠FEB = 62^{\circ}$,则$∠EDB$的度数为(
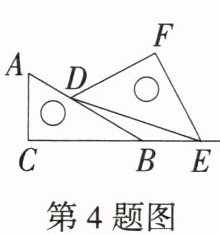
A. $12^{\circ}$
B. $13^{\circ}$
C. $17^{\circ}$
D. $18^{\circ}$
B
)
A. $12^{\circ}$
B. $13^{\circ}$
C. $17^{\circ}$
D. $18^{\circ}$
答案:
B 根据题意得,∠DEF = 45°,∠ABC = 30°,
∵∠FEB = 62°,
∴∠BED = ∠FEB - ∠DEF = 62° - 45° = 17°,
∵∠ABC = 30°,
∴∠EDB = ∠ABC - ∠BED = 30° - 17° = 13°. 故选 B.
∵∠FEB = 62°,
∴∠BED = ∠FEB - ∠DEF = 62° - 45° = 17°,
∵∠ABC = 30°,
∴∠EDB = ∠ABC - ∠BED = 30° - 17° = 13°. 故选 B.
5. 某数学兴趣小组在学校操场上进行实地测量.如图,在$A处测得建筑物C在南偏西57^{\circ}$的方向上,在$B处测得建筑物C在南偏西20^{\circ}$的方向上.在建筑物$C处测得A$,$B两处的视角∠C$的度数为( )

A. $67^{\circ}$
B. $57^{\circ}$
C. $47^{\circ}$
D. $37^{\circ}$

A. $67^{\circ}$
B. $57^{\circ}$
C. $47^{\circ}$
D. $37^{\circ}$
答案:
D 如图,

∵AM // BN,
∴∠ADB = ∠A = 57°,
∴∠C = ∠ADB - ∠CBD = 57° - 20° = 37°. 故选 D.
D 如图,

∵AM // BN,
∴∠ADB = ∠A = 57°,
∴∠C = ∠ADB - ∠CBD = 57° - 20° = 37°. 故选 D.
6. 如图,在$△ABC$中,点$D$,$E分别在边AB$,$AC$上,将$△ADE沿DE折叠至△FDE$的位置,点$A的对应点为F$.若$∠A = 15^{\circ}$,$∠BDF = 120^{\circ}$,则$∠CED$的度数为(
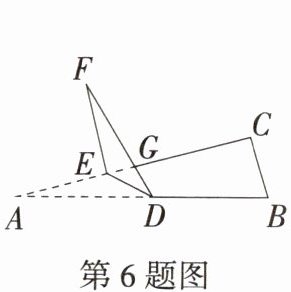
A. $30^{\circ}$
B. $40^{\circ}$
C. $45^{\circ}$
D. $50^{\circ}$
C
)
A. $30^{\circ}$
B. $40^{\circ}$
C. $45^{\circ}$
D. $50^{\circ}$
答案:
C
∵∠BDF = 120°,
∴∠ADF = 180° - ∠BDF = 60°,由折叠的性质可得∠ADE = ∠FDE = $\frac{1}{2}$∠ADF = 30°,
∵∠A = 15°,
∴∠CED = ∠ADE + ∠A = 45°. 故选 C.
∵∠BDF = 120°,
∴∠ADF = 180° - ∠BDF = 60°,由折叠的性质可得∠ADE = ∠FDE = $\frac{1}{2}$∠ADF = 30°,
∵∠A = 15°,
∴∠CED = ∠ADE + ∠A = 45°. 故选 C.
7. 将一张三角形纸片$EFG$按如图所示的方式摆放,已知$AB // CD$,顶点$F$,$G分别落在直线AB$,$CD$上,$GE交AB于点H$,$GE平分∠FGD$.若$∠EFG = 90^{\circ}$,$∠E = 35^{\circ}$,则$∠EFB$的度数为______
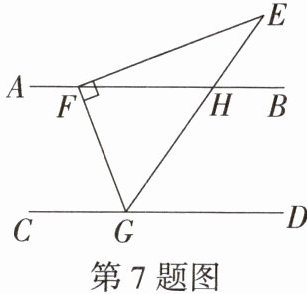
20°
.
答案:
答案 20°
解析
∵在△EFG中,∠EFG = 90°,∠E = 35°,
∴∠EGF = 90° - ∠E = 55°.
∵GE平分∠FGD,
∴∠EGD = ∠EGF = 55°.
∵AB // CD,
∴∠EHB = ∠EGD = 55°.
∵∠EHB = ∠EFB + ∠E,
∴∠EFB = ∠EHB - ∠E = 55° - 35° = 20°.
解析
∵在△EFG中,∠EFG = 90°,∠E = 35°,
∴∠EGF = 90° - ∠E = 55°.
∵GE平分∠FGD,
∴∠EGD = ∠EGF = 55°.
∵AB // CD,
∴∠EHB = ∠EGD = 55°.
∵∠EHB = ∠EFB + ∠E,
∴∠EFB = ∠EHB - ∠E = 55° - 35° = 20°.
8. 学科 特色 多解法 如图,在$△ABC$中,$D是BC$边上一点,$∠1 = ∠2$,$∠3 = ∠4$,$∠BAC = 75^{\circ}$,求$∠DAC$的度数.
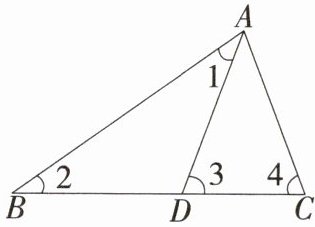

40°
答案:
解析 【解法一】设∠1 = ∠2 = x,则∠4 = ∠3 = ∠1 + ∠2 = 2x.
∵∠BAC = 75°,
∴∠2 + ∠4 = 180° - 75° = 105°,即x + 2x = 105°,解得x = 35°,
∴∠1 = 35°,
∴∠DAC = ∠BAC - ∠1 = 75° - 35° = 40°.
【解法二】设∠DAC = y,则∠1 = ∠2 = 75° - y,∠3 = ∠4 = $\frac{1}{2}$(180° - y).
∵∠3 = ∠1 + ∠2,
∴$\frac{1}{2}$(180° - y) = 75° - y + 75° - y,解得y = 40°. 故∠DAC = 40°.
∵∠BAC = 75°,
∴∠2 + ∠4 = 180° - 75° = 105°,即x + 2x = 105°,解得x = 35°,
∴∠1 = 35°,
∴∠DAC = ∠BAC - ∠1 = 75° - 35° = 40°.
【解法二】设∠DAC = y,则∠1 = ∠2 = 75° - y,∠3 = ∠4 = $\frac{1}{2}$(180° - y).
∵∠3 = ∠1 + ∠2,
∴$\frac{1}{2}$(180° - y) = 75° - y + 75° - y,解得y = 40°. 故∠DAC = 40°.
9. 如图,$△ABC$中,$AD \perp BC于点D$,$BE平分∠ABC$,若$∠ABC = 64^{\circ}$,$∠AEB = 70^{\circ}$.求$∠CAD$的度数.


52°
答案:
解析
∵BE平分∠ABC,
∴∠ABC = 2∠EBC = 64°,
∴∠EBC = 32°,
∵AD ⊥ BC,
∴∠ADB = ∠ADC = 90°,
∵∠C = ∠AEB - ∠EBC = 70° - 32° = 38°,
∴∠CAD = 90° - 38° = 52°.
∵BE平分∠ABC,
∴∠ABC = 2∠EBC = 64°,
∴∠EBC = 32°,
∵AD ⊥ BC,
∴∠ADB = ∠ADC = 90°,
∵∠C = ∠AEB - ∠EBC = 70° - 32° = 38°,
∴∠CAD = 90° - 38° = 52°.
查看更多完整答案,请扫码查看


