《2025年5年中考3年模拟八年级数学上册人教版》

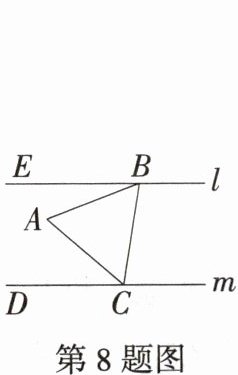
8.「2024山东泰安中考,★☆」如图,直线$l// m$,等边三角形$ABC的两个顶点B$,$C分别落在直线l$,$m$上,若$∠ABE = 21^{\circ}$,则$∠ACD$的度数是( )

A.$45^{\circ}$
B.$39^{\circ}$
C.$29^{\circ}$
D.$21^{\circ}$

答案：
B 如图，过点A作AF//l，

∵直线l//m，
∴AF//m，
∵△ABC是等边三角形，
∴∠BAC=60°，
∵AF//l，
∴∠BAF=∠ABE，
∵∠ABE=21°，
∴∠BAF=21°，
∴∠CAF=∠BAC−∠BAF=60°−21°=39°，
∵AF//m，
∴∠ACD=∠CAF=39°。故选B。

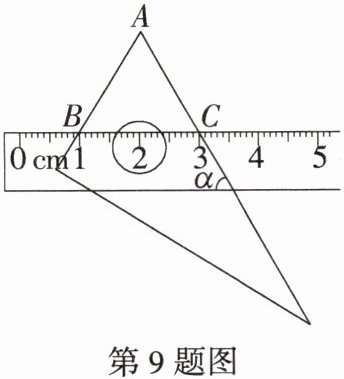
9.「2023江西中考,★☆」将含$30^{\circ}$角的直角三角尺和直尺按如图所示的方式放置,已知$∠α = 60^{\circ}$,点$B$,$C表示的刻度分别为1cm$,$3cm$,则线段$AB$的长为____2$cm$。

答案： 答案 2
解析
∵直尺的两对边相互平行，
∴∠ACB=∠α=60°，
∵∠A=60°，
∴∠ABC=180°−60°−60°=60°，
∴∠A=∠ABC=∠ACB，
∴△ABC是等边三角形，
∴AB=BC=3−1=2(cm)。

10.「★☆」如图,在$\triangle ABC$中,$∠ABC = 60^{\circ}$,$AB = 5$,$BE平分\triangle ABC的外角∠ABD$,$AE// BD交BE于E$,则$\triangle ABE$的周长是____15。

答案： 答案 15
解析
∵∠ABC=60°，
∴∠ABD=180°−60°=120°，
∵BE平分∠ABD，
∴∠ABE=∠DBE=60°，
∵AE//BD，
∴∠EAB=∠ABC=60°，
∴△ABE是等边三角形，
∴BE=AE=AB=5，
∴△ABE的周长是AB+BE+AE=15。

11.「2025山东聊城期末,★☆」如图所示的是某种落地灯的简易示意图,已知悬杆的$CD部分的长度与支杆BC$的长度相等,点$E在DC$的延长线上,且$∠BCE = 2∠BCD$,若$CD的长度为30cm$,则此时$B$,$D$两点之间的距离为____

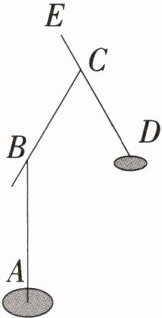
$cm$。

答案：
答案 30
解析 如图，连接BD，

∵∠BCE=2∠BCD，∠BCD+∠BCE=180°，
∴∠BCD=60°，
∵BC=CD，
∴△BCD是等边三角形，
∴BD=CD=30cm，
∴B，D两点之间的距离为30cm。

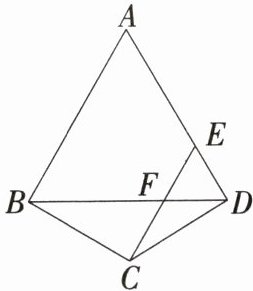
12.「2025河南开封期末,★☆」如图,在四边形$ABCD$中,$AB = AD$,$CB = CD$,$∠A = 60^{\circ}$,点$E为AD$上一点,连接$BD$,$CE交于点F$,$CE// AB$。
(1)判断$\triangle DEF$的形状,并说明理由。
(2)若$AD = 12$,$CE = 7$,求$CF$的长。

答案：
解析
(1)△DEF是等边三角形。理由：
∵AB=AD，∠A=60°，
∴△ABD为等边三角形，
∴∠ADB=∠ABD=60°，
∵CE//AB，
∴∠DEF=∠A=60°，∠EFD=∠ABD=60°，
∴△DEF是等边三角形。
(2)如图，连接AC交BD于点O，
∵AB=AD，CB=CD，
∴AC垂直平分BD，
∴AO⊥BD，
∴∠BAO=∠DAO=30°，
∵CE//AB，
∴∠ACE=∠BAO=∠DAO，
∴AE=CE=7，
∴DE=AD−AE=12−7=5，
∵△DEF是等边三角形，
∴EF=DE=5，
∴CF=CE−EF=2。

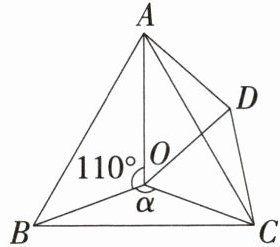
13.新几何直观「2025河南信阳期中」如图,点$O是等边\triangle ABC$内的一点,$D是\triangle ABC$外的一点,$∠AOB = 110^{\circ}$,$∠BOC = α$,$\triangle BOC≌\triangle ADC$,连接$OD$。
(1)求证：$\triangle OCD$是等边三角形。
(2)当$α = 150^{\circ}$时,试判断$\triangle AOD$的形状,并说明理由。
$\triangle AOD$是直角三角形。
(3)当$α$为多少度时,$\triangle AOD$是等腰三角形？
当$α=$110°或125°或140°时,$\triangle AOD$是等腰三角形。

答案： 解析
(1)证明：
∵△BOC≌△ADC，
∴∠BCO=∠ACD，OC=DC，
∵△ABC是等边三角形，
∴∠ACB=60°，
∴∠OCD=60°，
∴△OCD是等边三角形。
(2)△AOD是直角三角形。理由如下：
∵△OCD是等边三角形，
∴∠ODC=60°，
∵△BOC≌△ADC，α=150°，
∴∠ADC=∠BOC=α=150°，
∴∠ADO=∠ADC−∠ODC=150°−60°=90°，
∴△AOD是直角三角形。
(3)
∵△OCD是等边三角形，
∴∠COD=∠ODC=60°。
∵∠AOB=110°，∠ADC=∠BOC=α，
∴∠AOD=360°−∠AOB−∠BOC−∠COD=360°−110°−α−60°=190°−α，∠ADO=∠ADC−∠ODC=α−60°，
∴∠OAD=180°−∠AOD−∠ADO=180°−(190°−α)−(α−60°)=50°。
①当∠AOD=∠ADO时，190°−α=α−60°，
∴α=125°。
②当∠AOD=∠OAD时，190°−α=50°，
∴α=140°。
③当∠ADO=∠OAD时，α−60°=50°，
∴α=110°。
综上所述，当α=110°或125°或140°时，△AOD是等腰三角形。