第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7. 「2023四川凉山州中考」如图,点 E,点 F 在 BC 上,$BE= CF,∠B= ∠C$,添加一个条件,不能证明$△ABF\cong △DCE$的是(
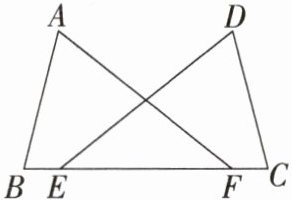
A. $∠A= ∠D$
B. $∠AFB= ∠DEC$
C. $AB= DC$
D. $AF= DE$
D
)
A. $∠A= ∠D$
B. $∠AFB= ∠DEC$
C. $AB= DC$
D. $AF= DE$
答案:
D
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∴当添加∠A=∠D时,利用AAS可得△ABF≌△DCE,故A不符合题意;当添加∠AFB=∠DEC时,利用ASA可得△ABF≌△DCE,故B不符合题意;当添加AB=DC时,利用SAS可得△ABF≌△DCE,故C不符合题意;当添加AF=DE时,无法证明△ABF≌△DCE,故D符合题意.故选D.
∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∴当添加∠A=∠D时,利用AAS可得△ABF≌△DCE,故A不符合题意;当添加∠AFB=∠DEC时,利用ASA可得△ABF≌△DCE,故B不符合题意;当添加AB=DC时,利用SAS可得△ABF≌△DCE,故C不符合题意;当添加AF=DE时,无法证明△ABF≌△DCE,故D符合题意.故选D.
8. 「2025河北沧州质检」如图,在$△ABC$中,$AB= AC,AB>BC$,点 D 在边 BC 上,$CD= 2BD$,点 E,F 在线段 AD 上,几何画板演示$∠1= ∠2= ∠BAC$,若$△ABC$的面积为 18,则$△ACF与△BDE$的面积之和为(
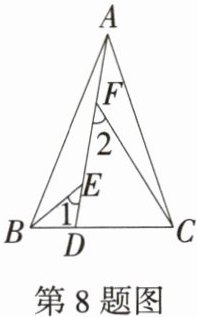
A. 6
B. 9
C. 12
D. 16
A
)
A. 6
B. 9
C. 12
D. 16
答案:
A
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,在△ABE和△CAF中,
$\left\{ \begin{array}{l} ∠ABE=∠CAF, \\ AB=AC, \\ ∠BAE=∠ACF, \end{array} \right. $
∴△ABE≌△CAF(ASA),
∴△ACF的面积=△ABE的面积,
∴△ACF与△BDE的面积之和=△ABE与△BDE的面积之和=△ABD的面积,
∵△ABC的面积为18,CD=2BD,
∴△ABD的面积= \frac{1}{3}×18=6,
∴△ACF与△BDE的面积之和=△ABD的面积=6,故选A.
∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠FCA+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠FCA,在△ABE和△CAF中,
$\left\{ \begin{array}{l} ∠ABE=∠CAF, \\ AB=AC, \\ ∠BAE=∠ACF, \end{array} \right. $
∴△ABE≌△CAF(ASA),
∴△ACF的面积=△ABE的面积,
∴△ACF与△BDE的面积之和=△ABE与△BDE的面积之和=△ABD的面积,
∵△ABC的面积为18,CD=2BD,
∴△ABD的面积= \frac{1}{3}×18=6,
∴△ACF与△BDE的面积之和=△ABD的面积=6,故选A.
9. 「2025广东东莞期中」海盗船是一种模拟海盗冒险场景的游乐项目.如图,当海盗船静止时,转轴 B 到地面的距离$BD= 15m$.当海盗船的船头在 A 处时,$AC⊥BD$,此时测得点 A 到地面的距离$AE= 9m$.当船头从 A 处摆动到$A'$处时,$A'B⊥AB$,则点$A'$到 BD 的距离为____.
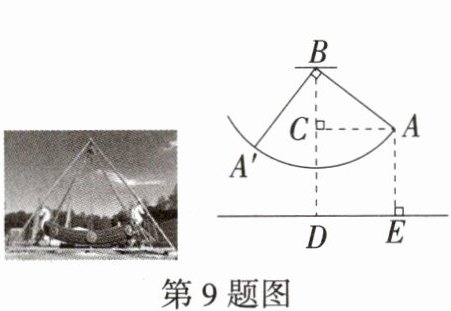

答案:
答案 6m
解析 如图,过点A'作A'F⊥BD于点F,

∵AC⊥BD,A'B⊥AB,
∴∠FBA'+∠FBA=∠CAB+∠FBA,
∴∠FBA'=∠CAB,
在△FBA'和△CAB中,
$\left\{ \begin{array}{l} ∠FBA'=∠CAB, \\ ∠A'FB=∠ACB=90°, \\ A'B=AB, \end{array} \right. $
∴△FBA'≌△CAB(AAS),
∴A'F=BC,又易知CD=AE=9m,
∴BC=BD−CD=6m,
∴A'F=6m,即点A'到BD的距离为6m.
答案 6m
解析 如图,过点A'作A'F⊥BD于点F,

∵AC⊥BD,A'B⊥AB,
∴∠FBA'+∠FBA=∠CAB+∠FBA,
∴∠FBA'=∠CAB,
在△FBA'和△CAB中,
$\left\{ \begin{array}{l} ∠FBA'=∠CAB, \\ ∠A'FB=∠ACB=90°, \\ A'B=AB, \end{array} \right. $
∴△FBA'≌△CAB(AAS),
∴A'F=BC,又易知CD=AE=9m,
∴BC=BD−CD=6m,
∴A'F=6m,即点A'到BD的距离为6m.
10. 「2024四川南充中考」如图,在$△ABC$中,点 D 为 BC 边的中点,过点 B 作$BE// AC$交 AD 的延长线于点 E.
(1)求证:$△BDE\cong △CDA$.
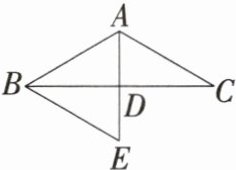
(2)若$AD⊥BC$,求证:$BA= BE$.
(1)求证:$△BDE\cong △CDA$.

证明:∵点D为BC的中点,∴BD=CD,∵BE//AC,∴∠EBD=∠C,∠E=∠CAD,在△BDE和△CDA中,$\left\{ \begin{array}{l} ∠EBD=∠C, \\ ∠E=∠CAD, \\ BD=CD, \end{array} \right. $∴△BDE≌△CDA(AAS).
(2)若$AD⊥BC$,求证:$BA= BE$.
证明:由(1)知△BDE≌△CDA,∴BE=CA,AD=DE,∵AD⊥BC,∴∠ADB=∠BDE=90°,在△ABD与△EBD中,$\left\{ \begin{array}{l} AD=DE, \\ ∠ADB=∠EDB, \\ BD=BD, \end{array} \right. $∴△ABD≌△EBD(SAS),∴BA=BE.
答案:
证明
(1)
∵点D为BC的中点,
∴BD=CD,
∵BE//AC,
∴∠EBD=∠C,∠E=∠CAD,
在△BDE和△CDA中,
$\left\{ \begin{array}{l} ∠EBD=∠C, \\ ∠E=∠CAD, \\ BD=CD, \end{array} \right. $
∴△BDE≌△CDA(AAS).
(2)由
(1)知△BDE≌△CDA,
∴BE=CA,AD=DE,
∵AD⊥BC,
∴∠ADB=∠BDE=90°,
在△ABD与△EBD中,
$\left\{ \begin{array}{l} AD=DE, \\ ∠ADB=∠EDB, \\ BD=BD, \end{array} \right. $
∴△ABD≌△EBD(SAS),
∴BA=BE.
(1)
∵点D为BC的中点,
∴BD=CD,
∵BE//AC,
∴∠EBD=∠C,∠E=∠CAD,
在△BDE和△CDA中,
$\left\{ \begin{array}{l} ∠EBD=∠C, \\ ∠E=∠CAD, \\ BD=CD, \end{array} \right. $
∴△BDE≌△CDA(AAS).
(2)由
(1)知△BDE≌△CDA,
∴BE=CA,AD=DE,
∵AD⊥BC,
∴∠ADB=∠BDE=90°,
在△ABD与△EBD中,
$\left\{ \begin{array}{l} AD=DE, \\ ∠ADB=∠EDB, \\ BD=BD, \end{array} \right. $
∴△ABD≌△EBD(SAS),
∴BA=BE.
11. 「」如图,在$Rt△ABC$中,$AB= BC,∠B= 90^{\circ }$,点 D 是 BC 边上一点,$DE⊥AD,CE⊥AC$,DE 和 CE 交于点 E.求证:$AD= DE$.
证明:如图,在 AB 上取一点 F,使$BF= BD$,连接 DF.$\because ∠ABC= 90^{\circ },\therefore △BFD$是等腰直角三角形,
$\therefore ∠BFD= 45^{\circ }$,
证明:如图,在 AB 上取一点 F,使$BF= BD$,连接 DF.$\because ∠ABC= 90^{\circ },\therefore △BFD$是等腰直角三角形,
$\therefore ∠BFD= 45^{\circ }$,
∵∠AFD+∠BFD=180°,∴∠AFD=135°,∵AB=BC,∠B=90°,CE⊥AC,∴∠ACB=45°,∠ACE=90°,∴∠DCE=45°+90°=135°,∴∠AFD=∠DCE,∵∠B=90°,∠ADE=90°,∴∠BAD+∠ADB=90°,∠ADB+∠CDE=90°,∴∠BAD=∠CDE.∵AB=BC,BF=BD,∴AF=DC,∴△AFD≌△DCE(ASA),∴AD=DE.
答案:
解析 补充证明过程如下:
∵∠AFD+∠BFD=180°,
∴∠AFD=135°,
∵AB=BC,∠B=90°,CE⊥AC,
∴∠ACB=45°,∠ACE=90°,
∴∠DCE=45°+90°=135°,
∴∠AFD=∠DCE,
∵∠B=90°,∠ADE=90°,
∴∠BAD+∠ADB=90°,∠ADB+∠CDE=90°,
∴∠BAD=∠CDE.
∵AB=BC,BF=BD,
∴AF=DC,
∴△AFD≌△DCE(ASA),
∴AD=DE.
∵∠AFD+∠BFD=180°,
∴∠AFD=135°,
∵AB=BC,∠B=90°,CE⊥AC,
∴∠ACB=45°,∠ACE=90°,
∴∠DCE=45°+90°=135°,
∴∠AFD=∠DCE,
∵∠B=90°,∠ADE=90°,
∴∠BAD+∠ADB=90°,∠ADB+∠CDE=90°,
∴∠BAD=∠CDE.
∵AB=BC,BF=BD,
∴AF=DC,
∴△AFD≌△DCE(ASA),
∴AD=DE.
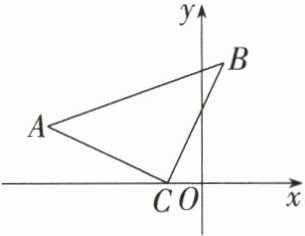
12. 新推理能力学科一线三垂直模型如图,在$△ACB$中,$∠ACB= 90^{\circ },AC= BC$,点 C 的坐标为$(-2,0)$,点 A 的坐标为$(-6,3)$,求点 B 的坐标.

答案:
解析 如图,过A作AD⊥x轴于D,过B作BE⊥x轴于E,

∴∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
$\left\{ \begin{array}{l} ∠ADC=∠CEB=90°, \\ ∠CAD=∠BCE, \\ AC=CB, \end{array} \right. $
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(−2,0),点A的坐标为(−6,3),
∴OC=2,AD=CE=3,OD=6,
∴CD=OD−OC=6−2=4,OE=CE−OC=3−2=1,
∴BE=CD=4,
∴点B的坐标为(1,4).
方法总结 一线三垂直模型:通常情况下利用的是两锐角互余与平角是180°,通过角的等量关系和已知的一组边相等证得两个直角三角形全等.
解析 如图,过A作AD⊥x轴于D,过B作BE⊥x轴于E,

∴∠ACD+∠CAD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
$\left\{ \begin{array}{l} ∠ADC=∠CEB=90°, \\ ∠CAD=∠BCE, \\ AC=CB, \end{array} \right. $
∴△ADC≌△CEB(AAS),
∴DC=BE,AD=CE,
∵点C的坐标为(−2,0),点A的坐标为(−6,3),
∴OC=2,AD=CE=3,OD=6,
∴CD=OD−OC=6−2=4,OE=CE−OC=3−2=1,
∴BE=CD=4,
∴点B的坐标为(1,4).
方法总结 一线三垂直模型:通常情况下利用的是两锐角互余与平角是180°,通过角的等量关系和已知的一组边相等证得两个直角三角形全等.
查看更多完整答案,请扫码查看


