第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 小明不小心把一块三角形的玻璃打碎成了三块,如图,他想到玻璃店配一块大小、形状完全一样的玻璃,则他应(
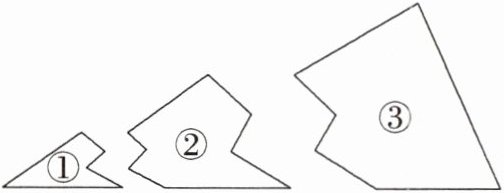
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
C
)
A. 带①去
B. 带②去
C. 带③去
D. 带①和②去
答案:
C 玻璃③包括了两角和它们的夹边,根据三角形全等的判定方法ASA可知,只有带③去才能配一块大小、形状完全一样的玻璃.故选C.
2. 如图,$AB// DE$,且$AB= DE,∠B= ∠E$,若$AF= 1,FD= 4$,则 FC 的长是____
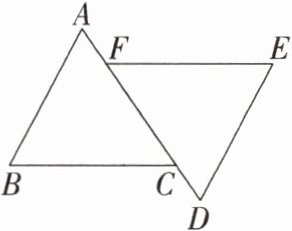
3
.
答案:
答案 3
解析
∵AB//DE,
∴∠A=∠D.在△ABC与△DEF中,
$\left\{ \begin{array}{l} ∠A=∠D, \\ AB=DE, \\ ∠B=∠E, \end{array} \right. $
∴△ABC≌△DEF(ASA),
∴AC=FD=4.
∵AF=1,
∴FC=AC−AF=4−1=3.故答案为3.
解析
∵AB//DE,
∴∠A=∠D.在△ABC与△DEF中,
$\left\{ \begin{array}{l} ∠A=∠D, \\ AB=DE, \\ ∠B=∠E, \end{array} \right. $
∴△ABC≌△DEF(ASA),
∴AC=FD=4.
∵AF=1,
∴FC=AC−AF=4−1=3.故答案为3.
3. 「2025甘肃武威期末」如图,四边形 ABCD 中,对角线 AC,BD 交于点 O,$AB= AC$,点 E 是 BD 上一点,且$∠ABD= ∠ACD,∠EAD= ∠BAC$.
(1)求证:$AE= AD$.
证明:∵∠BAC=∠EAD,
∴∠BAC−∠EAC=∠EAD−∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{ \begin{array}{l} ∠ABD=∠ACD, \\ AB=AC, \\ ∠BAE=∠CAD, \end{array} \right. $
∴△ABE≌△ACD(ASA),
∴AE=AD.
(2)若$BD= 8,DC= 5$,求 ED 的长.
解:∵△ABE≌△ACD,
∴BE=CD,
∵BD=8,DC=5,
∴ED=BD−BE=BD−CD=8−5=
(1)求证:$AE= AD$.
证明:∵∠BAC=∠EAD,
∴∠BAC−∠EAC=∠EAD−∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{ \begin{array}{l} ∠ABD=∠ACD, \\ AB=AC, \\ ∠BAE=∠CAD, \end{array} \right. $
∴△ABE≌△ACD(ASA),
∴AE=AD.
(2)若$BD= 8,DC= 5$,求 ED 的长.
解:∵△ABE≌△ACD,
∴BE=CD,
∵BD=8,DC=5,
∴ED=BD−BE=BD−CD=8−5=
3
.
答案:
解析
(1)证明:
∵∠BAC=∠EAD,
∴∠BAC−∠EAC=∠EAD−∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{ \begin{array}{l} ∠ABD=∠ACD, \\ AB=AC, \\ ∠BAE=∠CAD, \end{array} \right. $
∴△ABE≌△ACD(ASA),
∴AE=AD.
(2)
∵△ABE≌△ACD,
∴BE=CD,
∵BD=8,DC=5,
∴ED=BD−BE=BD−CD=8−5=3.
(1)证明:
∵∠BAC=∠EAD,
∴∠BAC−∠EAC=∠EAD−∠EAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
$\left\{ \begin{array}{l} ∠ABD=∠ACD, \\ AB=AC, \\ ∠BAE=∠CAD, \end{array} \right. $
∴△ABE≌△ACD(ASA),
∴AE=AD.
(2)
∵△ABE≌△ACD,
∴BE=CD,
∵BD=8,DC=5,
∴ED=BD−BE=BD−CD=8−5=3.
4. 「2025湖北荆州联考」如图,已知$△ABC$的六个元素,则甲、乙、丙三个三角形中和$△ABC$全等的是(
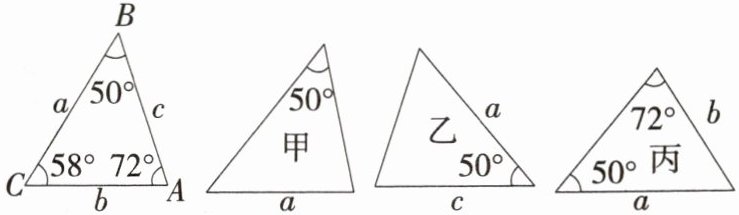
A. 甲、乙
B. 乙、丙
C. 甲、丙
D. 乙
B
)
A. 甲、乙
B. 乙、丙
C. 甲、丙
D. 乙
答案:
B 甲不符合三角形全等的判定定理,即三角形甲和△ABC不全等;可通过SAS判定三角形乙和△ABC全等;可通过AAS判定三角形丙和△ABC全等.故选B.
5. 如图,在$△ACD$中,$∠CAD= 90^{\circ },AC= 5,AD= 12,AB// CD$,点 E 是 CD 上一点,BE 交 AD 于点 F,若$AB= DE$,则图中阴影部分的面积为(
A. 30
B. 40
C. 45
D. 60
30
)A. 30
B. 40
C. 45
D. 60
答案:
A
∵AB//CD,
∴∠BAD=∠D,
在△BAF和△EDF中,
$\left\{ \begin{array}{l} ∠BFA=∠EFD, \\ ∠BAD=∠D, \\ AB=DE, \end{array} \right. $
∴△BAF≌△EDF(AAS),
∴S_{△BAF}=S_{△EDF},
∴题图中阴影部分的面积=S_{四边形ACEF}+S_{△BAF}=S_{△ACD}= \frac{1}{2}AC·AD= \frac{1}{2}×5×12=30.故选A.
∵AB//CD,
∴∠BAD=∠D,
在△BAF和△EDF中,
$\left\{ \begin{array}{l} ∠BFA=∠EFD, \\ ∠BAD=∠D, \\ AB=DE, \end{array} \right. $
∴△BAF≌△EDF(AAS),
∴S_{△BAF}=S_{△EDF},
∴题图中阴影部分的面积=S_{四边形ACEF}+S_{△BAF}=S_{△ACD}= \frac{1}{2}AC·AD= \frac{1}{2}×5×12=30.故选A.
6. 「2024江苏镇江中考」如图,$∠C= ∠D= 90^{\circ },∠CBA= ∠DAB$.
(1)求证:$△ABC\cong △BAD$.
(2)若$∠DAB= 70^{\circ }$,则$∠CAB= $____
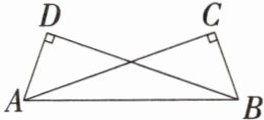
(1)求证:$△ABC\cong △BAD$.
(2)若$∠DAB= 70^{\circ }$,则$∠CAB= $____
20
$^{\circ }$.
答案:
解析
(1)证明:在△ABC和△BAD中,
$\left\{ \begin{array}{l} ∠C=∠D=90°, \\ ∠CBA=∠DAB, \\ AB=BA, \end{array} \right. $
∴△ABC≌△BAD(AAS).
(2)20.详解:
∵∠DAB=70°,∠D=90°,
∴∠DBA=90°−70°=20°,
由
(1)知△ABC≌△BAD,
∴∠CAB=∠DBA=20°,故答案为20.
(1)证明:在△ABC和△BAD中,
$\left\{ \begin{array}{l} ∠C=∠D=90°, \\ ∠CBA=∠DAB, \\ AB=BA, \end{array} \right. $
∴△ABC≌△BAD(AAS).
(2)20.详解:
∵∠DAB=70°,∠D=90°,
∴∠DBA=90°−70°=20°,
由
(1)知△ABC≌△BAD,
∴∠CAB=∠DBA=20°,故答案为20.
查看更多完整答案,请扫码查看


