《2025年5年中考3年模拟八年级数学下册人教版》

1.(2024山东潍坊期中)下列各式是二次根式的是（M8216001） （ ）
A.$\sqrt{3}$
B.$\sqrt{-2}$
C.$\sqrt{-\pi}$
D.$\sqrt[3]{3}$

答案： A：$\sqrt{3}$符合二次根式的定义，是二次根式，因为 -2 ＜ 0，所以$\sqrt{-2}$无意义，因为 -π ＜ 0，所以$\sqrt{-π}$无意义，$\sqrt[3]{3}$含有三次根号，不是二次根式，故选 A。

2.若式子$\sqrt{a}$是二次根式,则$a$的值不可以是 （ ）
A.0
B.-3
C.2
D.4

答案： B：
∵式子$\sqrt{a}$是二次根式，
∴ a ≥ 0，只有选项 B 中的 -3 ＜ 0，故选 B。

3.下列6个式子中,二次根式有（M8216001）（ ）
(1)$-\sqrt{\frac{1}{5}}$;(2)$\sqrt{-2025}$;(3)$-\sqrt{a^{2}+5}$;(4)$\sqrt[3]{9}$;
(5)$\sqrt{(-\frac{1}{2})^{2}}$;(6)$\sqrt{2 - m}(m＞2)$.
A.2个
B.3个
C.4个
D.5个

答案： B：根据二次根式的定义可知 -$\sqrt{\frac{1}{5}}$是二次根式；$\sqrt{-2025}$不是二次根式；-$\sqrt{a^{2}+5}$是二次根式；$\sqrt[3]{9}$含有三次根号，不是二次根式；$\sqrt{(-\frac{1}{2})^{2}}$是二次根式；$\sqrt{2 - m}$（m ＞ 2）不是二次根式。综上所述，是二次根式的有
(1)
(3)
(5)，共 3 个。故选 B。

4.若$\sqrt[|x - 2|]{x - 1}$是二次根式,则$x$的值为 （ ）
A.0
B.1
C.2
D.4

答案： D：
∵$\sqrt[|x - 2|]{x - 1}$是二次根式，
∴ |x - 2| = 2，即 x - 2 = 2 或 x - 2 = -2，
∴ x = 4 或 x = 0，
∵ x - 1 ≥ 0，
∴ x ≥ 1，
∴ x = 4，故选 D。

5.(2024浙江金华四校联考)已知正方体的表面积为24$dm^{2}$,则这个正方体的棱长为________.

答案： 答案：2 dm 解析：设这个正方体的棱长为 x dm（x ＞ 0），根据题意得 6x² = 24，
∴ x = $\sqrt{24÷6}$ = $\sqrt{4}$ = 2，
∴这个正方体的棱长为 2 dm。

6.(2024云南中考)若$\sqrt{x}$在实数范围内有意义,则实数$x$的取值范围是 （ ）
A.$x\geq0$
B.$x\leq0$
C.$x＞0$
D.$x＜0$

答案： A：根据题意得 x ≥ 0。故选 A。

7.(2024江西南昌期末改编)当$x = 2$时,下列二次根式没有意义的是 （ ）
A.$\sqrt{2 + x}$
B.$\sqrt{2 - x}$
C.$\sqrt{3 - x}$
D.$\sqrt{x - 4}$

答案： D：当 x = 2 时，$\sqrt{2 + x}$ = $\sqrt{4}$ = 2，$\sqrt{2 - x}$ = 0，$\sqrt{3 - x}$ = 1，故选项 A、B、C 不符合题意；当 x = 2 时，x - 4 = 2 - 4 = -2 ＜ 0，即$\sqrt{x - 4}$没有意义，故选项 D 符合题意。故选 D。

8.(2024山东潍坊期中)下列二次根式中,字母$a$的取值范围是全体实数的是 （ ）

A.$\sqrt{a}$
B.$\sqrt{a - 1}$
C.$\sqrt{\frac{1}{a + 1}}$
D.$\sqrt{(a - 1)^{2}}$

答案： D：
∵ (a - 1)² ≥ 0 恒成立，
∴ a 的取值范围为全体实数，
∴ D 选项正确，故选 D。

9.(2023湖南永州中考)已知$x$为正整数,写出一个使$\sqrt{x - 3}$在实数范围内没有意义的$x$值：________.

答案： 答案：1（答案也可以是 2） 解析：要使$\sqrt{x - 3}$在实数范围内没有意义，则 x - 3 ＜ 0，
∴ x ＜ 3，
∵ x 为正整数，
∴ x = 1，2（任选一个即可）。

10.已知$\sqrt{2m + 16}$是整数,则满足条件的$m$的最小值为________.

答案： 答案：-8 解析：由题意可知 2m + 16 ≥ 0，且$\sqrt{2m + 16}$为整数，
∴当 2m + 16 = 0 时，m 的值最小，此时 m = -8，
∴满足条件的 m 的最小值为 -8。

11.教材变式·P3T2 当$x$是怎样的实数时,下列各式在实数范围内有意义?
(1)$\sqrt{2 - 3x}$. (2)$\sqrt{2x^{2}+3}$.
(3)$\frac{\sqrt{x + 5}}{x - 2}$. (4)$\sqrt{x + 3}+x^{-2}$.

答案： 解析：
(1)由 2 - 3x ≥ 0 得 x ≤ $\frac{2}{3}$，所以当 x ≤ $\frac{2}{3}$时，$\sqrt{2 - 3x}$在实数范围内有意义。
(2)因为 2x² ≥ 0，所以 2x² + 3 ≥ 3 ＞ 0，所以当 x 取全体实数时，$\sqrt{2x^{2}+3}$在实数范围内有意义。
(3)由题意可知$\begin{cases}x + 5 ≥ 0 \\ x - 2 ≠ 0\end{cases}$，解得 x ≥ -5 且 x ≠ 2，所以当 x ≥ -5 且 x ≠ 2 时，$\frac{\sqrt{x + 5}}{x - 2}$在实数范围内有意义。
(4)由 x + 3 ≥ 0 且 x ≠ 0 得 x ≥ -3 且 x ≠ 0，所以当 x ≥ -3 且 x ≠ 0 时，$\sqrt{x + 3}+x^{-2}$在实数范围内有意义。

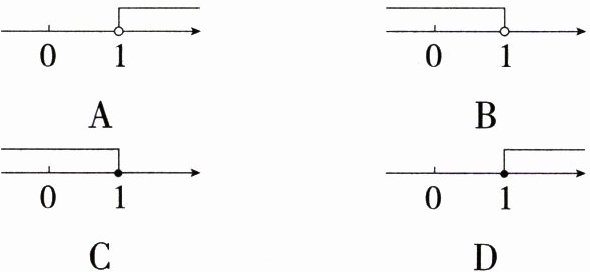
12.(2024云南昭通三模,7,★★☆)若$\frac{\sqrt{x - 1}}{x - 1}$有意义,则实数$x$的取值范围在数轴上表示正确的是 （ ）

答案：
A：由于$\frac{\sqrt{x - 1}}{x - 1}$有意义，则 x - 1 ≥ 0 且 x - 1 ≠ 0，即 x - 1 ＞ 0，所以 x ＞ 1，将 x ＞ 1 在数轴上表示如下：故选 A。