第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025北京房山期末改编」如图,$\triangle EFG \cong \triangle NMH, EF = 2.1\mathrm{cm}, EH = 1.1\mathrm{cm}, NH = 3.3\mathrm{cm}$,则线段 HG 的长度是 (

A.2.1 cm
B.3.3 cm
C.2.2 cm
D.1.1 cm
C
)
A.2.1 cm
B.3.3 cm
C.2.2 cm
D.1.1 cm
答案:
C
∵△EFG≌△NMH,
∴NH=EG=3.3cm,
∵EH=1.1cm,
∴HG=EG−EH=2.2cm.故选C.
∵△EFG≌△NMH,
∴NH=EG=3.3cm,
∵EH=1.1cm,
∴HG=EG−EH=2.2cm.故选C.
2.「2025天津和平期末」如图,在$∠AOB$的两边上,分别取$OM = ON$,再分别过点 M,N 作 OA,OB 的垂线,交点为 P,画射线 OP,则 OP 平分$∠AOB$的依据是 (

A.SAS
B.SSS
C.HL
D.AAS
C
)
A.SAS
B.SSS
C.HL
D.AAS
答案:
C 在Rt△OMP和Rt△ONP中, $\left\{\begin{array}{l} OP = OP, \\ OM = ON, \end{array}\right.$
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP = ∠NOP,
∴OP是∠AOB的平分线.故选C.
∴Rt△OMP≌Rt△ONP(HL),
∴∠MOP = ∠NOP,
∴OP是∠AOB的平分线.故选C.
3.如图,已知$AB // CF$,E 为 DF 的中点,若$AB = 13\mathrm{cm}, CF = 6\mathrm{cm}$,则 BD 的长为 (

A.6 cm
B.7 cm
C.12 cm
D.13 cm
B
)
A.6 cm
B.7 cm
C.12 cm
D.13 cm
答案:
B
∵AB//CF,E为DF的中点,
∴∠ADE = ∠EFC,DE = EF.在△ADE和△CFE中, $\left\{\begin{array}{l} \angle ADE = \angle EFC, \\ DE = EF, \\ \angle AED = \angle FEC, \end{array}\right.$
∴△ADE≌△CFE(ASA),
∴AD = CF = 6cm,
∵AB = 13cm,
∴BD = 13 - 6 = 7(cm).故选B.
∵AB//CF,E为DF的中点,
∴∠ADE = ∠EFC,DE = EF.在△ADE和△CFE中, $\left\{\begin{array}{l} \angle ADE = \angle EFC, \\ DE = EF, \\ \angle AED = \angle FEC, \end{array}\right.$
∴△ADE≌△CFE(ASA),
∴AD = CF = 6cm,
∵AB = 13cm,
∴BD = 13 - 6 = 7(cm).故选B.
4.「2025浙江杭州期末」如图,在$\triangle ABC$中,$∠B = ∠C = 50^{\circ}, BD = CF, BE = CD$,则$∠EDF$的度数是 (

A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$30^{\circ}$
B
)
A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$30^{\circ}$
答案:
B 在△BDE与△CFD中, $\left\{\begin{array}{l} BD = CF, \\ \angle B = \angle C, \\ BE = CD, \end{array}\right.$
∴△BDE≌△CFD(SAS),
∴∠BDE = ∠CFD,
∴∠EDF = 180° - (∠BDE + ∠CDF) = 180° - (∠CFD + ∠CDF) = 180° - (180° - ∠C) = 50°,故选B.
∴△BDE≌△CFD(SAS),
∴∠BDE = ∠CFD,
∴∠EDF = 180° - (∠BDE + ∠CDF) = 180° - (∠CFD + ∠CDF) = 180° - (180° - ∠C) = 50°,故选B.
5.「2025广东广州期末」如图,$\triangle ABC$的两外角的平分线 BP,CP 交于点 P,$PE ⊥ AC$交 AC 的延长线于点 E.若$\triangle ABC$的面积为 10,$\triangle BPC$的面积为 7,$PE = 4$,则$\triangle ABC$的周长为 ( )

A.8
B.10
C.11
D.12

A.8
B.10
C.11
D.12
答案:
D 如图,连接AP,过点P作PF⊥BC于F,PG⊥AB交AB的延长线于G,
∵△ABC的两外角的平分线BP,CP交于点P,PE⊥AC,PF⊥BC,PG⊥AG,
∴PG = PF = PE = 4,
∵△BPC的面积为7,
∴$\frac{1}{2}$BC×4 = 7,
∴BC = $\frac{7}{2}$,
∵△ABC的面积为10,
∴$\frac{1}{2}$AB×4 + $\frac{1}{2}$AC×4 - 7 = 10,
∴AB + AC = $\frac{17}{2}$,
∴△ABC的周长 = AB + AC + BC = $\frac{17}{2}$ + $\frac{7}{2}$ = 12.故选D.
D 如图,连接AP,过点P作PF⊥BC于F,PG⊥AB交AB的延长线于G,
∵△ABC的两外角的平分线BP,CP交于点P,PE⊥AC,PF⊥BC,PG⊥AG,
∴PG = PF = PE = 4,
∵△BPC的面积为7,
∴$\frac{1}{2}$BC×4 = 7,
∴BC = $\frac{7}{2}$,
∵△ABC的面积为10,
∴$\frac{1}{2}$AB×4 + $\frac{1}{2}$AC×4 - 7 = 10,
∴AB + AC = $\frac{17}{2}$,
∴△ABC的周长 = AB + AC + BC = $\frac{17}{2}$ + $\frac{7}{2}$ = 12.故选D.

6.如图,在$\triangle ABC$中,AC = BC,过点 B 作射线 BF,在射线 BF 上取一点 E,连接 AE,使得∠CBF =

∠CAE,过点 C 作射线 BF 的垂线,垂足为 D,若DE = 2, AE = 4,则 BD 的长度为 ( )
A.7
B.6
C.4
D.2

∠CAE,过点 C 作射线 BF 的垂线,垂足为 D,若DE = 2, AE = 4,则 BD 的长度为 ( )
A.7
B.6
C.4
D.2
答案:
B 如图,连接CE,过点C作CM⊥AE交AE的延长线于M.
∵CD⊥BF,CM⊥AM,
∴∠CDB = ∠CMA = 90°,在△CDB与△CMA中, $\left\{\begin{array}{l} \angle CDB = \angle CMA, \\ \angle CBD = \angle CAM, \\ CB = AC, \end{array}\right.$
∴△CDB≌△CMA(AAS),
∴CM = CD,BD = AM,在Rt△CED与Rt△CEM中, $\left\{\begin{array}{l} CE = CE, \\ CD = CM, \end{array}\right.$
∴Rt△CED≌Rt△CEM(HL),
∴DE = EM = 2,
∴BD = AM = AE + EM = 4 + 2 = 6,故选B.
B 如图,连接CE,过点C作CM⊥AE交AE的延长线于M.
∵CD⊥BF,CM⊥AM,
∴∠CDB = ∠CMA = 90°,在△CDB与△CMA中, $\left\{\begin{array}{l} \angle CDB = \angle CMA, \\ \angle CBD = \angle CAM, \\ CB = AC, \end{array}\right.$
∴△CDB≌△CMA(AAS),
∴CM = CD,BD = AM,在Rt△CED与Rt△CEM中, $\left\{\begin{array}{l} CE = CE, \\ CD = CM, \end{array}\right.$
∴Rt△CED≌Rt△CEM(HL),
∴DE = EM = 2,
∴BD = AM = AE + EM = 4 + 2 = 6,故选B.

7.「2024山东德州中考」如图,C 是 AB 的中点,且$CD = BE$,请添加一个条件:

AD = CE(答案不唯一)
,使得$\triangle ACD \cong \triangle CBE$.
答案:
答案 AD = CE(答案不唯一)解析 可添加AD = CE,理由如下:
∵C是AB的中点,
∴AC = CB,又
∵CD = BE,AD = CE,
∴△ACD≌△CBE(SSS),故答案为AD = CE(答案不唯一).
∵C是AB的中点,
∴AC = CB,又
∵CD = BE,AD = CE,
∴△ACD≌△CBE(SSS),故答案为AD = CE(答案不唯一).
8.「2025广东惠州期末」如图,$∠ACB = ∠ACD, CB = CD$,DA 的延长线交 BC 于点 E,若$∠EAC = 49^{\circ}$,则$∠BAE = $____

82
____$^{\circ}$.
答案:
答案 82解析 在△ABC和△ADC中, $\left\{\begin{array}{l} AC = AC, \\ \angle ACB = \angle ACD, \\ CB = CD, \end{array}\right.$
∴△ABC≌△ADC(SAS),
∴∠B = ∠D,∠DAC = ∠BAC,
∵∠EAC = 49°,
∴∠DAC = 180° - 49° = 131°,
∴∠BAC = 131°,
∴∠BAE = ∠BAC - ∠EAC = 82°,故答案为82.
∴△ABC≌△ADC(SAS),
∴∠B = ∠D,∠DAC = ∠BAC,
∵∠EAC = 49°,
∴∠DAC = 180° - 49° = 131°,
∴∠BAC = 131°,
∴∠BAE = ∠BAC - ∠EAC = 82°,故答案为82.
9.「2025天津期末」如图,$CB ⊥ AD, AE ⊥ CD$,垂足分别为 B,E,AE,BC 相交于点 F,若$AB = BC = 16, CF = 8$,连接 DF,则图中阴影部分的面积为____

32
.
答案:
答案 32解析
∵CB⊥AD,AE⊥CD,
∴∠ABF = ∠CBD = ∠FEC = 90°,
∵∠AFB = ∠EFC,
∴∠A = ∠C,在△ABF和△CBD中, $\left\{\begin{array}{l} \angle ABF = \angle CBD, \\ AB = CB, \\ \angle A = \angle C, \end{array}\right.$
∴△ABF≌△CBD(ASA),
∴BF = BD,
∵BF = BC - CF = 16 - 8 = 8,
∴BD = 8,
∴题图中阴影部分的面积 = $\frac{1}{2}$FC·BD = $\frac{1}{2}$×8×8 = 32.故答案为32.
∵CB⊥AD,AE⊥CD,
∴∠ABF = ∠CBD = ∠FEC = 90°,
∵∠AFB = ∠EFC,
∴∠A = ∠C,在△ABF和△CBD中, $\left\{\begin{array}{l} \angle ABF = \angle CBD, \\ AB = CB, \\ \angle A = \angle C, \end{array}\right.$
∴△ABF≌△CBD(ASA),
∴BF = BD,
∵BF = BC - CF = 16 - 8 = 8,
∴BD = 8,
∴题图中阴影部分的面积 = $\frac{1}{2}$FC·BD = $\frac{1}{2}$×8×8 = 32.故答案为32.
10.「2025山东临沂月考」如图,$CA ⊥ AB$,垂足为点 A,射线$BM ⊥ AB$,垂足为点 B,$AB = 15\mathrm{cm}, AC = 6\mathrm{cm}$.动点 E 从 A 点出发以$3\mathrm{cm}/s$的速度沿射线 AN 运动,动点 D 在射线 BM 上,随着 E 点的运动而运动,始终保持$ED = CB$.若点 E 的运动时间为$t\mathrm{s}(t > 0)$,则当以 B,E,D 为顶点的三角形与$\triangle ACB$全等时,$t = $____.


答案:
答案 3或7或10解析 ①当E在线段AB上,AC = BE时,△ACB≌△BED,
∵AC = 6cm,
∴BE = 6cm,
∴AE = AB - BE = 15 - 6 = 9(cm),
∴点E的运动时间为9÷3 = 3(s).②当E在BN上,AC = BE时,△ACB≌△BED,如图1所示,
∵AC = 6cm,
∴BE = 6cm,
∴AE = AB + BE = 15 + 6 = 21(cm).
∴点E的运动时间为21÷3 = 7(s).③当E在BN上,AB = BE时,△ACB≌△BDE,如图2所示,
∴AE = AB + BE = 15 + 15 = 30(cm),
∴点E的运动时间为30÷3 = 10(s).④当E在线段AB上,AB = BE时,△ACB≌△BDE,这时E在A点未动,因此运动时间为0s,不符合题意.故答案为3或7或10.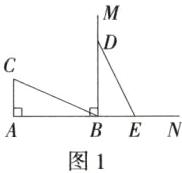

答案 3或7或10解析 ①当E在线段AB上,AC = BE时,△ACB≌△BED,
∵AC = 6cm,
∴BE = 6cm,
∴AE = AB - BE = 15 - 6 = 9(cm),
∴点E的运动时间为9÷3 = 3(s).②当E在BN上,AC = BE时,△ACB≌△BED,如图1所示,
∵AC = 6cm,
∴BE = 6cm,
∴AE = AB + BE = 15 + 6 = 21(cm).
∴点E的运动时间为21÷3 = 7(s).③当E在BN上,AB = BE时,△ACB≌△BDE,如图2所示,
∴AE = AB + BE = 15 + 15 = 30(cm),
∴点E的运动时间为30÷3 = 10(s).④当E在线段AB上,AB = BE时,△ACB≌△BDE,这时E在A点未动,因此运动时间为0s,不符合题意.故答案为3或7或10.


查看更多完整答案,请扫码查看


