《2025年5年中考3年模拟八年级数学上册人教版》

10. 如图,在三角形纸片ABC中,$∠A= 60^{\circ },∠B= 80^{\circ }$,将纸片的一角折叠,使点C落在$△ABC外的点C'$处.若$∠2= 35^{\circ }$,则$∠1$的度数为( )

A.$115^{\circ }$
B.$105^{\circ }$
C.$95^{\circ }$
D.$85^{\circ }$

答案：
10.A　如图,记AC与C'D交于点G,
∵∠A = 60°,∠B = 80°,
∴∠C = 180°−∠A−∠B = 180°−60°−80° = 40°,又
∵将三角形纸片的一角折叠,使点C落在△ABC外的点C'处，
∴∠C' = ∠C = 40°,
∵∠2 = 35°,
∴∠C'GE = 180°−∠C'−∠2 = 105°,
∴∠AGD = 105°,
∴∠1 = 360°−60°−80°−105° = 115°。故选A.

11. 如图,在$△ABC$中,若$DE// BC,FG// AC,∠BDE= 120^{\circ },∠DFG= 115^{\circ }$,则$∠C= $______55$^{\circ }$.

答案： 11.答案　55
解析
∵DE//BC,∠BDE = 120°,
∴∠B = 180°−120° = 60°,
∵FG//AC,∠DFG = 115°,
∴∠A = 180°−115° = 65°,
∵∠A + ∠B + ∠C = 180°,
∴∠C = 180°−∠B−∠A = 55°。

12. 当三角形中一个内角β是另外一个内角α的$\frac {1}{2}$时,我们称此三角形为“友好三角形”,其中α是这个“友好三角形”的“友好角”.如果一个“友好三角形”中有一个内角为$54^{\circ }$,那么这个“友好三角形”的“友好角”α的度数为54°或108°或84°.

答案： 12.答案　54°或108°或84°
解析　
(1)当α = 54°时,“友好角”α的度数为54°;
(2)当β = 54°时,由题意得α = 54°÷0.5 = 108°。
∴“友好角”α的度数为108°;
(3)当54°角既不是角α也不是角β时，
∵α + β + 54° = 180°,
∴α + $\frac{1}{2}$α + 54° = 180°,
∴α = 84°。
∴“友好角”α的度数为84°。故答案为54°或108°或84°。

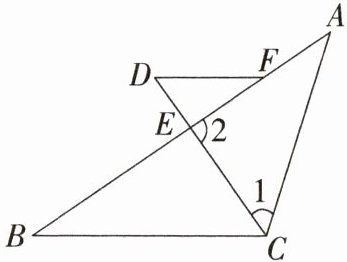
13. 如图,在$△ABC$中,CD平分$∠ACB$,CD交边AB于点E,在AE上取点F,连接DF,使$∠D= ∠1$.
(1)求证：$DF// BC$.
(2)当$∠A= 36^{\circ },∠DFE= 34^{\circ }$时,求$∠2$的度数.

(1)证明:∵CD平分∠ACB,∴∠DCB = ∠1,∵∠D = ∠1,∴∠DCB = ∠D,∴DF//BC。
(2)∵DF//BC,∠DFE = 34°,∴∠B = ∠DFE = 34°,在△ABC中,∠A = 36°,∠B = 34°,∴∠ACB = 180°−36°−34° = 110°,∵CD平分∠ACB,∴∠1 = $\frac{1}{2}$∠ACB = 55°,∴∠2 = 180°−36°−55° = 89°。

答案： 13.解析　
(1)证明:
∵CD平分∠ACB,
∴∠DCB = ∠1,
∵∠D = ∠1,
∴∠DCB = ∠D,
∴DF//BC。
(2)
∵DF//BC,∠DFE = 34°,
∴∠B = ∠DFE = 34°,在△ABC中,∠A = 36°,∠B = 34°,
∴∠ACB = 180°−36°−34° = 110°,
∵CD平分∠ACB,
∴∠1 = $\frac{1}{2}$∠ACB = 55°,
∴∠2 = 180°−36°−55° = 89°。

14. 已知,如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称为“8字形”.试解答下列问题：
(1)在图1中,请直接写出$∠A$、$∠B$、$∠C$、$∠D$之间的数量关系：______∠A + ∠D = ∠B + ∠C.
(2)仔细观察,在图2中,“8字形”的个数为______6.
(3)在图2中,若$∠D= 40^{\circ },∠B= 36^{\circ },∠DAB和∠BCD$的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N,利用(1)的结论,试求$∠P$的度数.
(4)当图2中$∠D和∠B$为任意角时,其他条件不变,试问$∠P与∠D$、$∠B$之间存在着怎样的数量关系？(直接写出结论即可)
______2∠P = ∠B + ∠D

答案： 14.解析　
(1)∠A + ∠D = ∠B + ∠C。
详解:在△AOD中,∠AOD = 180°−(∠A + ∠D),
在△BOC中,∠BOC = 180°−(∠B + ∠C),
∵∠AOD = ∠BOC,
∴180°−(∠A + ∠D)=180°−(∠B + ∠C),
∴∠A + ∠D = ∠B + ∠C。
(2)6.
详解:交点有点M、O、N,
以M为交点的“8”字形有1个,△AMD与△CMP;
以O为交点的“8”字形有4个,△AOD与△COB,△AOM与△CON,△AOM与△COB,△AOD与△CON;以N为交点的“8”字形有1个,△ANP与△CNB。
∴“8字形”共有6个。
(3)
∵∠D = 40°,∠B = 36°,
∴∠OAD + 40° = ∠OCB + 36°,
∴∠OCB−∠OAD = 4°,
∵AP和CP分别是∠DAB和∠BCD的平分线，
∴∠DAM = $\frac{1}{2}$∠OAD,∠PCM = $\frac{1}{2}$∠OCB,
又
∵∠DAM + ∠D = ∠PCM + ∠P,
∴∠P = ∠DAM + ∠D−∠PCM = ∠D−$\frac{1}{2}$(∠OCB−∠OAD)=40°−$\frac{1}{2}$×4° = 38°。
(4)2∠P = ∠B + ∠D。
详解:根据
(1)中的结论得,∠OAD + ∠D = ∠OCB + ∠B,∠DAM + ∠D = ∠PCM + ∠P,
∴∠OCB−∠OAD = ∠D−∠B,∠PCM−∠DAM = ∠D−∠P,
∵AP和CP分别是∠DAB和∠BCD的平分线，
∴∠DAM = $\frac{1}{2}$∠OAD,∠PCM = $\frac{1}{2}$∠OCB,
∴$\frac{1}{2}$(∠D−∠B)=∠D−∠P,
整理得,2∠P = ∠B + ∠D。