《2025年5年中考3年模拟八年级数学上册人教版》

7. 如图所示,在一条河的两岸有两个村庄,现要在河上建一座桥,桥的方向与河岸垂直,设河的宽度不变,试问：桥架在何处,才能使从 A 到 B 的距离最短？

答案：
解析 如图，作$BB'$垂直于河岸GH，且$BB'$等于河宽，连接$AB'$，与河岸EF交于P，将$PB'$沿与河岸垂直的方向平移，得到DB，连接PD，则$PD // BB'$且$PD = BB'$.
利用平移可知$PB' = BD$. 根据“两点之间，线段最短”，可知路径$A \to P \to D \to B$最短. 故桥架在PD处符合题意.
　　　　　　

8. 「2025 河北廊坊期中,★☆」如图,l 是 $ \triangle ABC $ 的边 AB 的垂直平分线,D 为垂足,E 是 l 上任意一点,且 $ AC = 5 $,$ BC = 8 $,$ AB = 6 $,则 $ \triangle AEC $ 的周长的最小值为( )

A. 6
B. 8
C. 11
D. 13

答案：
D 如图，连接BE，$\because l$是$\triangle ABC$的边AB的垂直平分线，$\therefore AE = BE$，$\therefore \triangle AEC$的周长$= AE + EC + AC = BE + EC + AC \geq BC + AC = 8 + 5 = 13$，故选D.
　　　　　　　　

9. 「2025 山东德州期中,★☆」如图,在五边形 ABCDE 中,$ \angle BAE = 142^{\circ} $,$ \angle B = \angle E = 90^{\circ} $,$ AB = BC $,$ AE = DE $,在 BC,DE 上分别找一点 M,N,使得 $ \triangle AMN $ 的周长最小,此时 $ \angle AMN + \angle ANM $ 的度数为( )

A. $ 76^{\circ} $
B. $ 84^{\circ} $
C. $ 96^{\circ} $
D. $ 109^{\circ} $

答案：
A 如图，延长AB至$A'$，使$A'B = AB$，延长AE至$A''$，使$A''E = AE$，连接$A'A''$分别交BC，DE于点M，N，易知此时$AM + MN + AN$的值最小，即$\triangle AMN$的周长最小，
　　　　　
$\because$ BC垂直平分$AA'$，DE垂直平分$AA''$，
$\therefore AM = A'M$，$AN = A''N$，
$\therefore$ 可设$\angle MAA' = \angle MA'A = x$，$\angle NAA'' = \angle NA''A = y$，
$\therefore \angle AMN = \angle MAA' + \angle MA'A = 2x$，$\angle ANM = \angle NAA'' + \angle NA''A = 2y$，
$\because$ 在$\triangle AA'A''$中，$x + y = 180^{\circ} - \angle BAE = 180^{\circ} - 142^{\circ} = 38^{\circ}$，
$\therefore \angle AMN + \angle ANM = 2x + 2y = 76^{\circ}$，
故选A.

10. 「2025 河南周口期中,★☆」如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD = 10 $,D 是 BC 的中点,EF 垂直平分 AB,交 AB 于点 E,交 AC 于点 F,在 EF 上确定一点 P,使 $ PB + PD $ 最小,则 $ PB + PD $ 的最小值为10.

答案： 答案 10
解析 当点P在AD与EF的交点处时，$PB + PD$取得最小值，为AD的长，$\because AD = 10$，$\therefore PB + PD$的最小值为10.

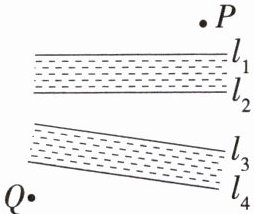
11. 「2025 四川泸州月考,★☆」如图,P,Q 两村之间隔着两条河,需要架设两座桥,桥与河岸垂直,设两条河的宽度相同,则桥建在何处才能使两村之间的路程最短？

答案：
解析 如图，作$PH \perp l_1$，使得$PG = GH =$河的宽度，连接QH交直线$l_4$于点F，作$FE \perp l_4$交直线$l_3$于点E，连接EG交直线$l_2$于点N，作$NM \perp l_2$交直线$l_1$于点M，连接PM，线路$P \to M \to N \to E \to F \to Q$即为两村之间的最短路线. $\therefore$ 桥建在MN和EF处才能使两村之间的路程最短.
　　　　　　　

12. 新推理能力 已知：M,N 分别是 $ \angle AOB $ 的边 OA,OB 上的定点.
(1) 如图 1,若 $ \angle O = \angle OMN $,过 M 作射线 $ MD // OB $,点 C 是射线 MD 上一动点,$ \angle MNC $ 的平分线 NE 交射线 OA 于 E 点,试探究 $ \angle MEN $ 与 $ \angle MCN $ 之间的数量关系.
(2) 如图 2,若 P 是线段 ON 上一动点,Q 是射线 MA 上一动点,$ \angle AOB = 20^{\circ} $,当 $ MP + PQ + QN $ 取得最小值时,求 $ \angle OPM + \angle OQN $ 的值.

答案：
解析 （1）设$\angle O = \angle OMN = \alpha$，$\therefore \angle MNB = 2\alpha$，
$\because MD // OB$，
$\therefore \angle AMD = \angle O = \alpha$，
$\because NE$平分$\angle MNC$，
$\therefore \angle MNE = \angle ENC$，
设$\angle MNE = \angle ENC = \beta$，$\therefore \angle CNB = 2\alpha - 2\beta$，
$\because MD // OB$，
$\therefore \angle MCN = \angle CNB = 2\alpha - 2\beta$，
$\because \angle EMC + \angle MEN = \angle ENC + \angle MCN$，
$\therefore \alpha + \angle MEN = \beta + 2\alpha - 2\beta$，
$\therefore \angle MEN = \alpha - \beta$，$\therefore 2\angle MEN = \angle MCN$.
（2）如图，作M点关于OB的对称点$M'$，N点关于OA的对称点$N'$，连接$M'N'$，与OB，OA分别交于点P，点Q，连接$ON'$，$OM'$，此时$MP + PQ + QN$的值最小，最小值为$M'N'$的长，
　　　　　
由对称性可知，$\angle OQN' = \angle OQN$，$\angle OPM' = \angle OPM$，
$\therefore \angle OPM' = \angle QPN = \angle AOB + \angle OQP = \angle AOB + 180^{\circ} - \angle OQN'$，
$\because \angle AOB = 20^{\circ}$，
$\therefore \angle OPM' = 200^{\circ} - \angle OQN'$，$\therefore$ 当$MP + PQ + QN$取得最小值时，$\angle OPM + \angle OQN = \angle OPM' + \angle OQN' = 200^{\circ}$.