《2025年5年中考3年模拟八年级数学上册人教版》

1.「2025 福建福州期末」下列各组中的三条线段,能组成三角形的是 (D)
A. 1,2,3
B. 1,2,4
C. 2,2,4
D. 4,5,6

答案： 1.D　1+2=3，不能组成三角形，故A不符合题意；
1+2＜4，不能组成三角形，故B不符合题意；
2+2=4，不能组成三角形，故C不符合题意；
4+5＞6，能组成三角形，故D符合题意.
故选D.

2.「2024 广西中考」端午节是中国传统节日,下列与端午节有关的文创图案中,是轴对称图形的是 (B)

答案： 2.B　因为B选项中的图形能找到这样的一条直线，使图形沿这条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形，故选B.

3. 如图,将$\triangle ABC$折叠,使 AC 边落在 AB 边上,展开后得到折痕 l,则 l 是$\triangle ABC$的 ( )

A. 中线
B. 边的垂直平分线
C. 高线
D. 角平分线

答案：
3.D　如图，依题意知∠CAD = ∠BAD，
∴l是△ABC的角平分线.故选D.

4.「2023 四川眉山中考」如图,$\triangle ABC$中,$AB= AC,∠A= 40^{\circ }$,则$∠ACD$的度数为 (C)

A. $70^{\circ }$
B. $100^{\circ }$
C. $110^{\circ }$
D. $140^{\circ }$

答案： 4.C
∵AB = AC，
∴∠B = ∠ACB，
∵∠A = 40°，
∴∠B = ∠ACB = $\frac{180^{\circ}-\angle A}{2} = \frac{180^{\circ}-40^{\circ}}{2} = 70^{\circ}$，
∵∠ACD是△ABC的一个外角，
∴∠ACD = ∠A + ∠B = 40°+70°=110°.故选C.

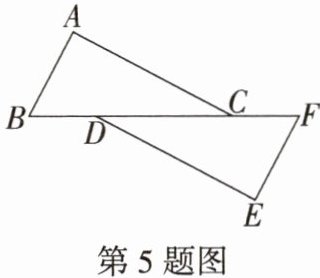
5.「2023 山东青岛育才中学期末」如图,点 B,D,C,F 在同一条直线上,$AB// EF,AB= EF,AC// DE$,如果$BF= 6,DC= 3$,那么 BD 的长等于 (B)

A. 1
B. $\frac {3}{2}$
C. 2
D. 3

答案： 5.B
∵AB//EF，
∴∠B = ∠F，
∵AC//DE，
∴∠ACB = ∠EDF，
在△ABC和△EFD中，$\begin{cases}\angle ACB = \angle EDF\\\angle B = \angle F\\AB = EF\end{cases}$，
∴△ABC≌△EFD(AAS)，
∴BC = FD，
∴BC - DC = FD - DC，
∴BD = FC，
∴BD = $\frac{1}{2}(BF - DC)=\frac{1}{2}\times(6 - 3)=\frac{3}{2}$.故选B.

6.「2025 河北沧州期末」如图,AD 是$\triangle ABC$的角平分线,$DE⊥AB$于点 E,$DF⊥AC$于点 F.若$S_{\triangle ABC}= 28,DE= 4,AB= 8$,则 AC 的长是 (6)

A. 8
B. 7
C. 6
D. 5

答案： 6.C
∵AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，
∴DF = DE = 4.
∵$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$，AB = 8，
∴$28=\frac{1}{2}\times8\times4+\frac{1}{2}\times AC\times4$，
∴AC = 6.故选C.

7.「2025 福建师大附中期末」如图所示的正方形网格中,像点 A、点 B 这样网格线的交点称为格点.以 AB 为边的等腰三角形 ABC 的三个顶点都是格点,这样的等腰三角形有 ( )

A. 10 个
B. 8 个
C. 6 个
D. 4 个

答案：
7.A　如图所示，分以下情况讨论：

①当AB为等腰△ABC的底边时，符合条件的C点有6个：$C_1$，$C_2$，$C_3$，$C_4$，$C_5$，$C_6$；
②当AB为等腰△ABC的一条腰时，符合条件的C点有4个：$C_7$，$C_8$，$C_9$，$C_{10}$.
∴满足条件的点C共有10个，故选A.

8. 如图,在$\triangle ACD和\triangle BCE$中,$CA= CB,AD= BE,CD= CE,∠ACE= 50^{\circ },∠BCD= 150^{\circ },AD$与 BE 相交于点 P,则$∠BPD$的度数为 (B)

A. $140^{\circ }$
B. $130^{\circ }$
C. $120^{\circ }$
D. $110^{\circ }$

答案： 8.B　在△ACD和△BCE中，$\begin{cases}AC = BC\\AD = BE\\CD = CE\end{cases}$，
∴△ACD≌△BCE(SSS)，
∴∠ACD = ∠BCE，∠A = ∠B，
∴∠BCA+∠ACE = ∠ACE+∠ECD，
∴∠ACB = ∠ECD = $\frac{1}{2}(\angle BCD - \angle ACE)$，
∵∠ACE = 50°，∠BCD = 150°，
∴∠ACB = $\frac{1}{2}\times(150^{\circ}-50^{\circ}) = 50^{\circ}$，
∵∠B+∠ACB = ∠A+∠APB，
∴∠APB = ∠ACB = 50°，
∴∠BPD = 180°−50°=130°，故选B.

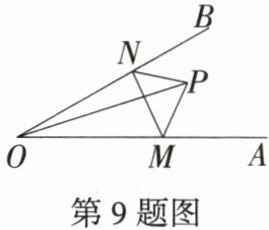
9. 如图,点 P 是$∠AOB$内任意一点,$OP= 5cm$,点 M 和点 N 分别是射线 OA 和射线 OB 上的动点,$\triangle PMN$周长的最小值是 5 cm,则$∠AOB$的度数是 ( )

A. $25^{\circ }$
B. $30^{\circ }$
C. $35^{\circ }$
D. $40^{\circ }$

答案：
9.B　分别作点P关于OA，OB的对称点D，C，连接CD，分别交OA，OB于点M，N，连接OC，OD，PM，PN，如图所示：

易知此时△PMN的周长取得最小值，为CD的长，
∵点P关于OA的对称点为D，点P关于OB的对称点为C，
∴OP = OD，∠DOA = ∠POA，OP = OC，∠COB = ∠POB，
∴OC = OP = OD，∠AOB = $\frac{1}{2}\angle COD$，
∵△PMN周长的最小值是5cm，OP = 5cm，
∴CD = OP，
∴OC = OD = CD，
∴△OCD是等边三角形，
∴∠COD = 60°，
∴∠AOB = 30°.故选B.

10. 如图,已知$\triangle ABC与\triangle CDE$都是等边三角形,点 B,C,D 在同一条直线上,AD 与 BE 相交于点 G,BE 与 AC 相交于点 F,AD 与 CE 相交于点 H,连接 FH. 给出下列结论:①$\triangle ACD\cong \triangle BCE$;②$∠AGB= 60^{\circ }$;③$BF= AH$;④$\triangle CFH$是等边三角形.其中正确结论的个数是 (D)

A. 1
B. 2
C. 3
D. 4

答案： 10.D
∵△ABC与△CDE都是等边三角形，
∴∠BCA = ∠DCE = 60°，AC = BC，CE = CD，
∴∠BCE = ∠ACD，在△BCE和△ACD中，$\begin{cases}BC = AC\\\angle BCE = \angle ACD\\CE = CD\end{cases}$，
∴△BCE≌△ACD(SAS)，故①正确；
∵△BCE≌△ACD，
∴∠CBF = ∠CAH，
∵∠BFC = ∠AFG，
∴∠AGB = ∠ACB = 60°，故②正确；
∵点B，C，D在同一条直线上，∠ACB = ∠ECD = 60°，
∴∠ACE = 180°−60°−60°=60°，
∴∠BCF = ∠ACH，在△BCF和△ACH中，$\begin{cases}\angle CBF = \angle CAH\\BC = AC\\\angle BCF = \angle ACH\end{cases}$，
∴△BCF≌△ACH(ASA)，
∴CF = CH，BF = AH，故③正确；
∵CF = CH，∠ACH = 60°，
∴△CFH是等边三角形，故④正确.故选D.