《2025年5年中考3年模拟八年级数学上册人教版》

1.「2024河北石家庄期末」如图,在$\triangle ABC$中,$AE$是角平分线,$AD$是高,$∠C= 40^{\circ },∠B= 70^{\circ },DF⊥AE$,垂足为$F$.
(1)求$∠CAE$的度数.35°
(2)求$∠ADF$的度数.75°

答案： 解析
(1) $\because \angle C = 40^{\circ}, \angle B = 70^{\circ}$，
$\therefore \angle BAC = 180^{\circ} - (\angle C + \angle B) = 70^{\circ}$，
$\because AE$ 是 $\angle BAC$ 的平分线，
$\therefore \angle CAE = \frac{1}{2}\angle BAC = 35^{\circ}$。
(2) $\because AD$ 是 $\triangle ABC$ 的高，
$\therefore \angle CAD = 90^{\circ} - \angle C = 50^{\circ}$，
$\therefore \angle DAE = \angle CAD - \angle CAE = 15^{\circ}$，
$\because DF \perp AE$，
$\therefore \angle ADF = 90^{\circ} - \angle DAE = 75^{\circ}$。

2.「2025河南新乡月考」已知$\triangle ABC$中,$∠B＞∠C$,射线$AE平分∠BAC$,点$F为射线AE$上一点,过点$F作FD⊥BC于点D$.
(1)若$∠B= 65^{\circ },∠C= 35^{\circ }$.
①如图1,当点$F与点A$重合时,$∠DAE= $____15°.
②如图2,当点$F在线段AE$上(不与端点重合)时,求$∠DFE$的度数.
(2)设$∠B= x,∠C= y$,如图3,当点$F在射线EF$上时(不与点$E$重合),直接写出$∠DFE$的度数.(用含$x、y$的式子表示)$\frac{1}{2}(x - y)$

答案： 解析
(1) ① $\because \angle BAC + \angle B + \angle C = 180^{\circ}, \angle B = 65^{\circ}$，$\angle C = 35^{\circ}$，
$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 65^{\circ} - 35^{\circ} = 80^{\circ}$，
$\because AE$ 平分 $\angle BAC$，
$\therefore \angle CAE = \angle BAE = \frac{1}{2}\angle BAC = 40^{\circ}$，
在 $Rt\triangle ACD$ 中，$\angle ADC = 90^{\circ}, \angle C = 35^{\circ}$，
$\therefore \angle DAC = 180^{\circ} - \angle ADC - \angle C = 180^{\circ} - 90^{\circ} - 35^{\circ} = 55^{\circ}$，
$\therefore \angle DAE = \angle DAC - \angle CAE = 55^{\circ} - 40^{\circ} = 15^{\circ}$，
故答案为 $15^{\circ}$。
② 由
(1) ① 知 $\angle CAE = 40^{\circ}$，
$\because \angle DEF$ 是 $\triangle AEC$ 的外角，$\angle C = 35^{\circ}$，
$\therefore \angle DEF = \angle C + \angle CAE = 35^{\circ} + 40^{\circ} = 75^{\circ}$，
在 $Rt\triangle DEF$ 中，$\angle FDE = 90^{\circ}$，
$\therefore \angle DFE = 180^{\circ} - \angle FDE - \angle DEF = 180^{\circ} - 90^{\circ} - 75^{\circ} = 15^{\circ}$。
(2) $\angle DFE = \frac{1}{2}(x - y)$。
详解：$\because \angle BAC + \angle B + \angle C = 180^{\circ}, \angle B = x, \angle C = y$，
$\therefore \angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - x - y$，
$\because AE$ 平分 $\angle BAC$，
$\therefore \angle CAE = \angle BAE = \frac{1}{2}\angle BAC = 90^{\circ} - \frac{1}{2}(x + y)$，
$\therefore \angle CEF = \angle CAE + \angle C = 90^{\circ} - \frac{1}{2}(x + y) + y = 90^{\circ} - \frac{1}{2}(x - y)$，
在 $Rt\triangle DEF$ 中，$\angle FDE = 90^{\circ}$，
$\therefore \angle DFE = 180^{\circ} - \angle DEF - \angle FDE = 180^{\circ} - \left[90^{\circ} - \frac{1}{2}(x - y)\right] - 90^{\circ} = \frac{1}{2}(x - y)$。

3.「2025广东东莞期中」在$\triangle ABC$中,$BD,CE分别是∠ABC,∠ACB$的平分线,$BD,CE相交于点P$.
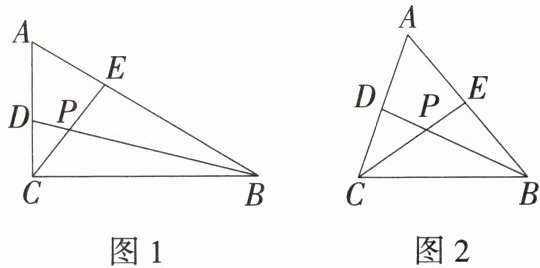
(1)如图1,若$∠A= 60^{\circ },∠ACB= 90^{\circ }$,则$∠BPC= $$120^{\circ}$.
(2)如图2,若$∠A= 60^{\circ },∠ACB$不是直角,求$∠BPC$的度数.
(3)有位同学在解答(1)(2)后得出$∠BPC= 90^{\circ }+\frac {1}{2}∠A$的规律,你认为正确吗? 请给出理由.

答案： 解析
(1) $\because \angle A = 60^{\circ}, \angle ACB = 90^{\circ}, \therefore$ 根据三角形的内角和定理得 $\angle ABC = 180^{\circ} - 60^{\circ} - 90^{\circ} = 30^{\circ}$，
$\because BD, CE$ 分别是 $\angle ABC, \angle ACB$ 的平分线，
$\therefore \angle PCB = \frac{1}{2}\angle ACB = 45^{\circ}, \angle PBC = \frac{1}{2}\angle ABC = 15^{\circ}$，
在 $\triangle PBC$ 中，根据三角形的内角和定理得，
$\angle BPC = 180^{\circ} - \angle PCB - \angle PBC = 180^{\circ} - 45^{\circ} - 15^{\circ} = 120^{\circ}$，
故答案为 $120^{\circ}$。
(2) $\because BD, CE$ 分别是 $\angle ABC, \angle ACB$ 的平分线，
$\therefore \angle ACB = 2\angle PCB, \angle ABC = 2\angle PBC$，
$\because$ 在 $\triangle ABC$ 中，$\angle A + \angle ABC + \angle ACB = 180^{\circ}, \angle A = 60^{\circ}$，
$\therefore \angle ABC + \angle ACB = 180^{\circ} - \angle A = 120^{\circ}$，
$\therefore 2\angle PCB + 2\angle PBC = 120^{\circ}$，
$\therefore \angle PCB + \angle PBC = 60^{\circ}$，
$\because$ 在 $\triangle PBC$ 中，$\angle BPC + \angle PCB + \angle PBC = 180^{\circ}$，
$\therefore \angle BPC = 180^{\circ} - (\angle PCB + \angle PBC) = 180^{\circ} - 60^{\circ} = 120^{\circ}$。
(3) 正确，理由如下：
$\because BD, CE$ 分别是 $\angle ABC, \angle ACB$ 的平分线，
$\therefore \angle PBC + \angle PCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180^{\circ} - \angle A) = 90^{\circ} - \frac{1}{2}\angle A$，
$\therefore \angle BPC = 180^{\circ} - (\angle PBC + \angle PCB) = 180^{\circ} - \left(90^{\circ} - \frac{1}{2}\angle A\right) = 90^{\circ} + \frac{1}{2}\angle A$。