《2025年5年中考3年模拟八年级数学上册人教版》

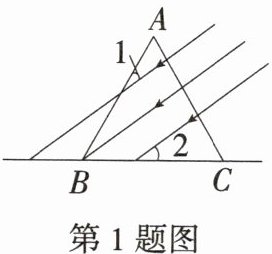
1.如图,一束太阳光线平行照射在放置于地面的等边$\triangle ABC$上,若$∠1 = 24^{\circ}$,则$∠2$的度数为( )

A.$24^{\circ}$
B.$36^{\circ}$
C.$48^{\circ}$
D.$56^{\circ}$

答案：
B 如图所示，
∵△ABC是等边三角形，
∴∠ABC=60°，
∴∠ABD=180°−∠ABC=120°，
∵∠1=∠BGD=24°，
∴∠BDG=180°−120°−24°=36°，
∵太阳光线平行，
∴DG//EF，
∴∠2=∠BDG=36°。故选B。

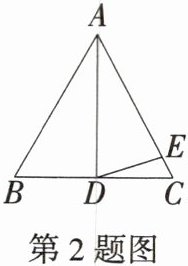
2.「2025贵州黔东南州期末」如图,$AD是等边\triangle ABC$的一条中线,若在边$AC上取一点E$,使得$AE = AD$,连接$DE$,则$∠EDC$的度数为(D)

A.$30^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$15^{\circ}$

答案： D
∵△ABC为等边三角形，
∴∠BAC=60°，
∵AD是等边△ABC的一条中线，
∴AD⊥BC，∠CAD=$\frac{1}{2}$∠BAC=30°，
∵AE=AD，
∴∠ADE=∠AED，
∵∠ADE+∠AED+∠CAD=180°，
∴∠ADE=75°，
∴∠EDC=90°−75°=15°。故选D。

3.学科一线三等特色角模型如图,点$D$,$E$,$F分别为等边\triangle ABC三边AB$,$BC$,$AC$上的动点,当$\triangle DEF$为等边三角形时,$AD = 3$,则线段$CF$的长为____3。

答案： 答案 3
解析
∵△ABC是等边三角形，
∴∠A=∠C=60°，
∴∠ADF+∠AFD=180°−∠A=120°，
∵△DEF是等边三角形，
∴DF=FE，∠DFE=60°，
∴∠AFD+∠CFE=180°−∠DFE=120°，
∴∠ADF=∠CFE，
∴△ADF≌△CFE(AAS)，
∴CF=AD=3。

4.学科教材特色变式如图,$\triangle ABC$是等边三角形,$BD是AC$边上的高,延长$BC至E$,连接$DE$,使$DB = DE$。
(1)求$∠BDE$的度数。120°
(2)求证：$\triangle CED$是等腰三角形。
证明：∵∠ACB=60°，∠E=30°，∴∠CDE=∠ACB−∠E=30°，∴∠CDE=∠E，∴CD=CE，∴△CED是等腰三角形。

答案： 解析
(1)
∵△ABC是等边三角形，
∴∠ACB=∠ABC=60°，
∵BD是AC边上的高，
∴∠DBE=30°，
∵DB=DE，
∴∠E=∠DBE=30°，
∴∠BDE=180°−30°−30°=120°。
(2)证明：
∵∠ACB=60°，∠E=30°，
∴∠CDE=∠ACB−∠E=30°，
∴∠CDE=∠E，
∴CD=CE，
∴△CED是等腰三角形。

5.「2025云南昆明期末」下列条件不能判定$\triangle ABC$是等边三角形的是(D)
A.$∠A = ∠B = ∠C$
B.$AB = BC$,$AC = BC$
C.$AB = BC$,$∠B = 60^{\circ}$
D.$AB = BC$,$∠A = ∠C$

答案： D A.
∵∠A=∠B=∠C，∠A+∠B+∠C=180°，
∴∠A=∠B=∠C=60°，
∴△ABC是等边三角形，故本选项不符合题意；B.
∵AB=BC，AC=BC，
∴AB=BC=AC，
∴△ABC是等边三角形，故本选项不符合题意；C.
∵AB=BC，∠B=60°，
∴△ABC是等边三角形，故本选项不符合题意；D.由AB=BC，∠A=∠C无法判定△ABC是等边三角形，故本选项符合题意。故选D。

6.「2025天津和平期末」如图,工人在某施工现场作业,有一个长为$1.6$米的梯子(图中$CM$)斜靠在墙上,此时梯子的倾斜角为$75^{\circ}$,如果梯子底端不动,顶端靠在对面的墙上,此时梯子(图中$CN$)的倾斜角为$45^{\circ}$,那么$MN$的长是1.6米。

答案： 答案 1.6
解析 由题意可得∠MCN=180°−∠ACM−∠BCN=60°，
∵CM=CN，
∴△CMN为等边三角形，
∴MN=CM=1.6米。

7.「2025江苏南京师大附中月考」如图,在$\triangle ABC$中,$AB = AC$,$∠BAC = 120^{\circ}$,$AB$、$AC边的垂直平分线分别交BC于点E$、$D$,连接$AE$、$AD$。求证：$\triangle AED$是等边三角形。
证明 ∵AB=AC，∠BAC=120°，∴∠B=∠C=$\frac{1}{2}$×(180°−120°)=30°，∵AB、AC边的垂直平分线分别交BC于点E、D，∴AE=BE，AD=CD，∴∠BAE=∠B=30°，∠CAD=∠C=30°，∴∠AED=∠B+∠BAE=60°，∠ADE=∠C+∠CAD=60°，∴∠DAE=180°−∠AED−∠ADE=60°，∴△ADE是等边三角形。

答案： 证明
∵AB=AC，∠BAC=120°，
∴∠B=∠C=$\frac{1}{2}$×(180°−120°)=30°，
∵AB、AC边的垂直平分线分别交BC于点E、D，
∴AE=BE，AD=CD，
∴∠BAE=∠B=30°，∠CAD=∠C=30°，
∴∠AED=∠B+∠BAE=60°，∠ADE=∠C+∠CAD=60°，
∴∠DAE=180°−∠AED−∠ADE=60°，
∴△ADE是等边三角形。