第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025浙江杭州期末」如图,在$\triangle ABC$中,$AB= AC$,$BD平分\angle ABC$,若$\angle A= 40^{\circ}$,则$\angle DBC$的度数为(
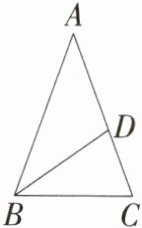
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$
B
)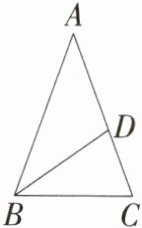
A.$30^{\circ}$
B.$35^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$
答案:
B $\because AB = AC$,$\angle A = 40^{\circ}$,$\therefore \angle ABC = \frac{1}{2} \times (180^{\circ} - 40^{\circ}) = 70^{\circ}$,$\because BD$平分$\angle ABC$,$\therefore \angle DBC = \frac{1}{2} \angle ABC = 35^{\circ}$。故选B。
2.如图,在$\triangle ABC$中,$AB= AD$,$\angle B= 2\angle C$,$\angle BAD= 32^{\circ}$,则$\angle C$的度数为(
A.$32^{\circ}$
B.$35^{\circ}$
C.$37^{\circ}$
D.$40^{\circ}$
37°
)
A.$32^{\circ}$
B.$35^{\circ}$
C.$37^{\circ}$
D.$40^{\circ}$
答案:
C $\because AB = AD$,$\therefore \angle B = \angle BDA = \frac{1}{2} \times (180^{\circ} - 32^{\circ}) = 74^{\circ}$,$\because \angle B = 2 \angle C$,$\therefore \angle C = \frac{1}{2} \angle B = 37^{\circ}$。故选C。
3.「2025北京门头沟期末」如图,在$\triangle ABC$中,$DE垂直平分AB$,垂足为$D$,交$BC于点E$,连接$AE$。如果$AE= AC$,$\angle B= 25^{\circ}$,那么$\angle C$的度数是____
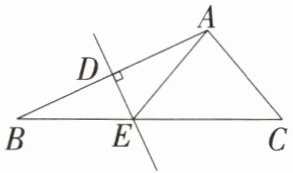
50°
。
答案:
答案 $50^{\circ}$
解析 $\because DE$垂直平分$AB$,$\therefore EA = EB$,$\therefore \angle B = \angle BAE = 25^{\circ}$,$\because \angle AEC$是$\triangle ABE$的一个外角,$\therefore \angle AEC = \angle B + \angle BAE = 50^{\circ}$,$\because AE = AC$,$\therefore \angle AEC = \angle C = 50^{\circ}$。
解析 $\because DE$垂直平分$AB$,$\therefore EA = EB$,$\therefore \angle B = \angle BAE = 25^{\circ}$,$\because \angle AEC$是$\triangle ABE$的一个外角,$\therefore \angle AEC = \angle B + \angle BAE = 50^{\circ}$,$\because AE = AC$,$\therefore \angle AEC = \angle C = 50^{\circ}$。
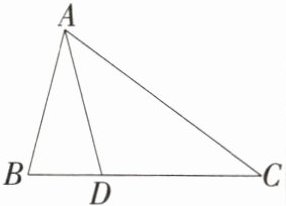
4.如图,点$D是BC$上的一点,若$\triangle ABC\cong\triangle ADE$,且$\angle B= 55^{\circ}$,则$\angle EAC= $
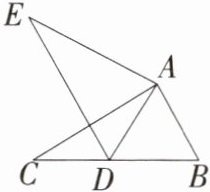
70
$^{\circ}$。
答案:
答案 $70$
解析 $\because \triangle ABC \cong \triangle ADE$,$\therefore AB = AD$,$\angle EAD = \angle CAB$,$\therefore \angle ADB = \angle B$,$\angle EAC = \angle DAB$。$\because \angle B = 55^{\circ}$,$\therefore \angle ADB = \angle B = 55^{\circ}$,$\therefore \angle DAB = 180^{\circ} - \angle ADB - \angle B = 70^{\circ}$,$\therefore \angle EAC = \angle DAB = 70^{\circ}$。
解析 $\because \triangle ABC \cong \triangle ADE$,$\therefore AB = AD$,$\angle EAD = \angle CAB$,$\therefore \angle ADB = \angle B$,$\angle EAC = \angle DAB$。$\because \angle B = 55^{\circ}$,$\therefore \angle ADB = \angle B = 55^{\circ}$,$\therefore \angle DAB = 180^{\circ} - \angle ADB - \angle B = 70^{\circ}$,$\therefore \angle EAC = \angle DAB = 70^{\circ}$。
5.易错题若等腰三角形中有一个角等于$40^{\circ}$,则这个等腰三角形顶角的度数为
$40^{\circ}$或$100^{\circ}$
。
答案:
答案 $40^{\circ}$或$100^{\circ}$
解析 $\because$等腰三角形中有一个角等于$40^{\circ}$,$\therefore$分两种情况讨论:①若顶角为$40^{\circ}$,则这个等腰三角形顶角的度数为$40^{\circ}$;②若底角为$40^{\circ}$,则这个等腰三角形顶角的度数为$180^{\circ} - 40^{\circ} \times 2 = 100^{\circ}$。$\therefore$这个等腰三角形顶角的度数为$40^{\circ}$或$100^{\circ}$。
易错警示 本题的易错之处是忽略分类讨论,因为题中没有指明已知角是顶角还是底角,所以要进行分类讨论。
解析 $\because$等腰三角形中有一个角等于$40^{\circ}$,$\therefore$分两种情况讨论:①若顶角为$40^{\circ}$,则这个等腰三角形顶角的度数为$40^{\circ}$;②若底角为$40^{\circ}$,则这个等腰三角形顶角的度数为$180^{\circ} - 40^{\circ} \times 2 = 100^{\circ}$。$\therefore$这个等腰三角形顶角的度数为$40^{\circ}$或$100^{\circ}$。
易错警示 本题的易错之处是忽略分类讨论,因为题中没有指明已知角是顶角还是底角,所以要进行分类讨论。
6.变式如图,在$\triangle ABC$中,点$D在BC$上,$AB= AC= CD$,且$AD= BD$。求$\triangle ABC$的三个内角的度数。
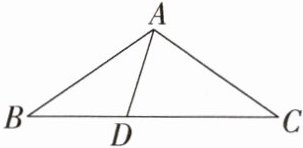
$\triangle ABC$的三个内角的度数分别是

$\triangle ABC$的三个内角的度数分别是
108°
,36°
,36°
。
答案:
解析 设$\angle B = x$,$\because AB = AC$,$\therefore \angle C = \angle B = x$,
$\because AD = BD$,$\therefore \angle BAD = \angle B = x$,
由三角形外角的性质得$\angle CDA = \angle B + \angle BAD = 2x$,
$\because AC = CD$,$\therefore \angle CAD = \angle CDA = 2x$,
$\because \angle C + \angle CAD + \angle CDA = 180^{\circ}$,
$\therefore x + 2x + 2x = 180^{\circ}$,解得$x = 36^{\circ}$,
$\therefore \angle C = 36^{\circ}$,$\angle B = 36^{\circ}$,
$\therefore \angle BAC = 180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}$。
$\therefore \triangle ABC$的三个内角的度数分别是$108^{\circ}$,$36^{\circ}$,$36^{\circ}$。
$\because AD = BD$,$\therefore \angle BAD = \angle B = x$,
由三角形外角的性质得$\angle CDA = \angle B + \angle BAD = 2x$,
$\because AC = CD$,$\therefore \angle CAD = \angle CDA = 2x$,
$\because \angle C + \angle CAD + \angle CDA = 180^{\circ}$,
$\therefore x + 2x + 2x = 180^{\circ}$,解得$x = 36^{\circ}$,
$\therefore \angle C = 36^{\circ}$,$\angle B = 36^{\circ}$,
$\therefore \angle BAC = 180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}$。
$\therefore \triangle ABC$的三个内角的度数分别是$108^{\circ}$,$36^{\circ}$,$36^{\circ}$。
7.「2025江苏苏州期中」如图,某园林中一亭子的顶端可看成等腰$\triangle ABC$,其中$AB= AC$,若$D是BC$边上的一点,则下列不能说明$BD= CD$的是(
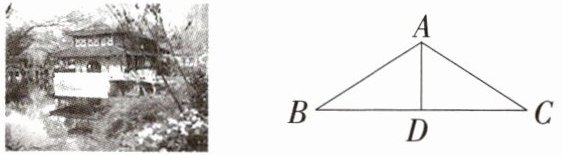
A.$AD\perp BC$
B.$\angle BAD= \angle CAD$
C.$\angle B= \angle C$
D.$\triangle ABD\cong\triangle ACD$
C
)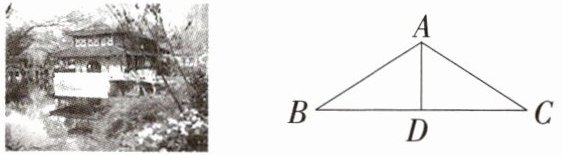
A.$AD\perp BC$
B.$\angle BAD= \angle CAD$
C.$\angle B= \angle C$
D.$\triangle ABD\cong\triangle ACD$
答案:
C A. 当$AB = AC$,$AD \perp BC$时,$AD$是$\triangle ABC$的中线,则$BD = CD$,不符合题意;B. 当$AB = AC$,$\angle BAD = \angle CAD$时,$AD$是$\triangle ABC$的中线,则$BD = CD$,不符合题意;C. 由已知不能判定$BD = CD$,符合题意;D. 当$\triangle ABD \cong \triangle ACD$时,$BD = CD$,不符合题意。故选C。
8.如图,在$\triangle ABC$中,$AB= AC$,$D$,$E分别是边BC$,$AC$上的点,连接$AD$,$BE$。若$AD和BE分别是\triangle ABC$的中线和角平分线,$\angle CAD= 20^{\circ}$,求$\angle CBE$的度数。
$\angle CBE$的度数为

$\angle CBE$的度数为
35°
。
答案:
解析 $\because AB = AC$,$AD$是$\triangle ABC$的中线,
$\therefore \angle BAD = \angle CAD = 20^{\circ}$,$\angle ABC = \angle ACB$,
$\therefore \angle ABC = \frac{1}{2} \times (180^{\circ} - 20^{\circ} - 20^{\circ}) = 70^{\circ}$,
$\because BE$是$\triangle ABC$的角平分线,
$\therefore \angle CBE = \frac{1}{2} \angle ABC = 35^{\circ}$。
$\therefore \angle BAD = \angle CAD = 20^{\circ}$,$\angle ABC = \angle ACB$,
$\therefore \angle ABC = \frac{1}{2} \times (180^{\circ} - 20^{\circ} - 20^{\circ}) = 70^{\circ}$,
$\because BE$是$\triangle ABC$的角平分线,
$\therefore \angle CBE = \frac{1}{2} \angle ABC = 35^{\circ}$。
查看更多完整答案,请扫码查看


