《2025年5年中考3年模拟八年级数学上册人教版》

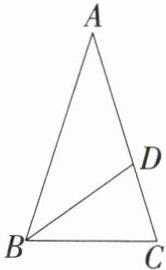
1.如图,在△ABC中,AB= AC,∠A= 36°,BD是△ABC的角平分线,则图中的等腰三角形共有(C)

A.1个
B.2个
C.3个
D.4个

答案： C
∵∠A = 36°, AB = AC,
∴∠ABC = ∠C = 72°, △ABC是等腰三角形.
∵BD是△ABC的角平分线，
∴∠ABD = ∠DBC = $\frac{1}{2}$∠ABC = 36°,
∴∠A = ∠ABD,
∴△ABD是等腰三角形.
∵∠DBC = 36°, ∠C = 72°,
∴∠BDC = 72°,
∴∠BDC = ∠C,
∴△BDC是等腰三角形.
综上，题图中的等腰三角形共有3个.故选C.

2.在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,则下列条件中,不能判定△ABC是等腰三角形的是(B)
A.∠A：∠B：∠C= 2：2：5
B.a：b：c= 3：4：5
C.a= 5,b= 6,c= 5
D.∠A= 40°,∠B= 100°

答案： B 选项A中，
∵∠A : ∠B : ∠C = 2 : 2 : 5，
∴∠A = ∠B,
∴△ABC是等腰三角形，
故A不符合题意；
选项B中，
∵a : b : c = 3 : 4 : 5,
∴a, b, c互不相等，
∴△ABC不是等腰三角形，故B符合题意；
选项C中，
∵a = 5, b = 6, c = 5,
∴a = c，
∴△ABC是等腰三角形，故C不符合题意；
选项D中，
∵∠A = 40°, ∠B = 100°，
∴∠C = 180° - ∠A - ∠B = 40°,
∴∠A = ∠C，
∴△ABC是等腰三角形，故D不符合题意.故选B.

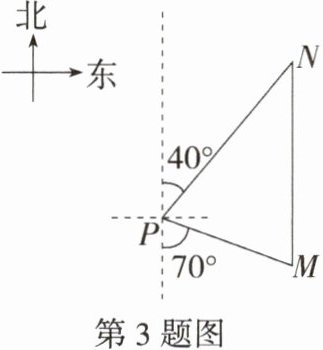
3.如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为______海里。

答案： 答案 80
解析 由题意知∠M = 70°, ∠N = 40°，
∴∠NPM = 180° - 70° - 40° = 70°,
∴∠NPM = ∠M，
∴NP = MN = 40×2 = 80(海里).

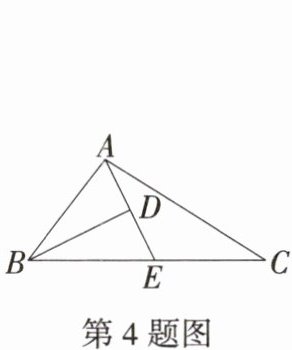
4.如图,在△ABC的BC边上截取BE= AB,连接AE,作△ABE的角平分线BD交AE于点D,若∠EAC= ∠C,BC= 9,AB= 5,则AD= 2。

答案： 答案 2
解析
∵BE = AB, BD平分∠ABE,
∴AD = DE，
∵∠EAC = ∠C,
∴EA = EC,
∵BC = 9, AB = 5,
∴CE = BC - BE = BC - AB = 9 - 5 = 4,
∴AD = DE = $\frac{1}{2}$AE = $\frac{1}{2}$CE = 2.

5.尺规作图：已知一个等腰三角形底边及底边上的高,求作这个等腰三角形。
已知：如图,线段a,h。
求作：△ABC,使AB= AC,且BC= a,高AD= h。
(要求：保留作图的痕迹,写出结论,但不要求写出作法)

答案：
解析 如图，作线段BC = a，作线段BC的垂直平分线DT，垂足为D，在射线DT上截取DA，使得DA = h，连接AB, AC，则△ABC即为所求.
　　

6.如图,在△ABC中,AB= AC,M、N分别是AB、AC边上的点,并且MN//BC。
(1)求证：△AMN是等腰三角形。
证明：∵AB = AC, ∴∠ABC = ∠C，∵MN // BC, ∴∠AMN = ∠ABC, ∠ANM = ∠C，∴∠AMN = ∠ANM, ∴AM = AN，∴△AMN是等腰三角形.
(2)点P是MN上的一点,并且BP平分∠ABC,求证：△BPM是等腰三角形。
证明：∵BP平分∠ABC, ∴∠MBP = ∠CBP，∵MN // BC, ∴∠MPB = ∠CBP，∴∠MBP = ∠MPB, ∴MB = MP，∴△BPM是等腰三角形.

答案： 证明 （1）
∵AB = AC,
∴∠ABC = ∠C，
∵MN // BC,
∴∠AMN = ∠ABC, ∠ANM = ∠C，
∴∠AMN = ∠ANM,
∴AM = AN，
∴△AMN是等腰三角形.
（2）
∵BP平分∠ABC,
∴∠MBP = ∠CBP，
∵MN // BC,
∴∠MPB = ∠CBP，
∴∠MBP = ∠MPB,
∴MB = MP，
∴△BPM是等腰三角形.

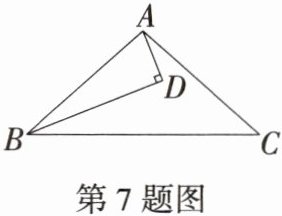
7.如图,在△ABC中,BD平分∠ABC,AD⊥BD,∠CAD= ∠C,若AB= 5,AD= 2,则BC的长为( )

A.6
B.7
C.8
D.9

答案：
D 如图，延长AD交BC于点E,
∵BD平分∠ABC, AD ⊥ BD,
∴∠ABD = ∠EBD, ∠ADB = ∠EDB = 90°，
∵BD = BD,
∴△ABD ≌ △EBD(ASA),
∴BA = BE = 5，
AD = ED = 2,
∴AE = 4,
∵∠CAD = ∠C,
∴EC = EA = 4，
∴BC = BE + EC = 9.故选D.

8.如图,在平面直角坐标系中有一点P(4,3),连接OP,OP= 5,在x轴上找一点Q,使△OPQ是以OP为腰的等腰三角形,则点Q的坐标不能是( )

A.(-5,0)
B.(5,0)
C.(8,0)
D.(25/8,0)

答案：
D 设点Q的坐标为(m, 0)，则OQ = |m|.
①若OQ = OP，则|m| = 5,
∴m = ±5；
②若PO = PQ，如图，过P作PH ⊥ x轴于H，

∴OH = QH = 4,
∴OQ = 8,
∴m = 8.
综上所述，点Q的坐标为(-5, 0)或(5, 0)或(8, 0).故选D.