第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025江苏常州期中」下列与如图所示的三角形全等的是(
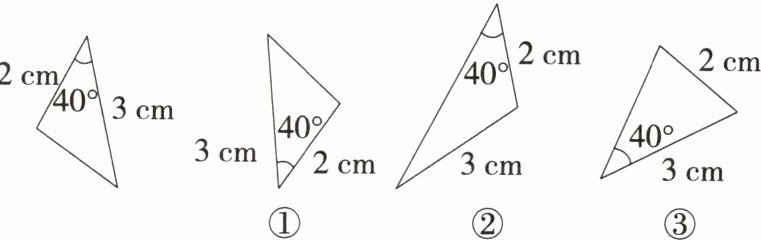
A.①②
B.②③
C.①③
D.只有①
D
)
A.①②
B.②③
C.①③
D.只有①
答案:
D 根据题图中数据,只能利用“SAS”判定①与已知三角形全等.
2.「2025湖北宜昌期中」如图,AC和BD相交于点O,OA= OC,OB= OD,下列说法错误的是(
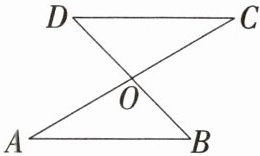
A.AB//CD
B.AB≠CD,AB//CD
C.AB= CD
D.AB= CD,AB//CD
B
)
A.AB//CD
B.AB≠CD,AB//CD
C.AB= CD
D.AB= CD,AB//CD
答案:
B 在△AOB和△COD中,$\left\{\begin{array}{l} OA=OC,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right.$
∴△AOB≌△COD(SAS),
∴∠A=∠C,AB=CD,
∴AB//CD,故A、C、D正确,不符合题意;B错误,符合题意.故选B.
∴△AOB≌△COD(SAS),
∴∠A=∠C,AB=CD,
∴AB//CD,故A、C、D正确,不符合题意;B错误,符合题意.故选B.
3.「2025北京东城期末」如图,点E,F在BC上,AB= CD,AF= DE,AF,DE相交于点G,若添加一个条件,可使得△ABF≌△DCE,则添加的条件可以是
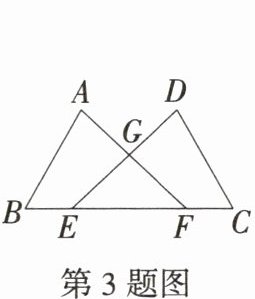
∠A=∠D(答案不唯一)
.
答案:
答案 ∠A=∠D(答案不唯一)
解析 添加∠A=∠D,在△ABF和△DCE中,$\left\{\begin{array}{l} AB=DC,\\ ∠A=∠D,\\ AF=DE,\end{array}\right.$
∴△ABF≌△DCE(SAS),故添加的条件可以是∠A=∠D(答案不唯一).
解析 添加∠A=∠D,在△ABF和△DCE中,$\left\{\begin{array}{l} AB=DC,\\ ∠A=∠D,\\ AF=DE,\end{array}\right.$
∴△ABF≌△DCE(SAS),故添加的条件可以是∠A=∠D(答案不唯一).
4.「2025河南洛阳期中改编」在生物实验课上,老师布置了“测量锥形瓶内部底面内径”的任务.小亮同学想到了以下方案:如图,用螺丝钉将两根长度相等的小棒AD,BC的中点O固定,利用全等三角形的性质,只要测得C,D之间的距离,就可知道内径AB的长.此方案中,判定△AOB和△DOC是全等三角形的依据是______

SAS
.
答案:
答案 SAS
解析 在△AOB和△DOC中,$\left\{\begin{array}{l} OB=OC,\\ ∠AOB=∠DOC,\\ OA=OD,\end{array}\right.$
∴△AOB≌△DOC(SAS).
解析 在△AOB和△DOC中,$\left\{\begin{array}{l} OB=OC,\\ ∠AOB=∠DOC,\\ OA=OD,\end{array}\right.$
∴△AOB≌△DOC(SAS).
5.「2025山东青岛月考」如图,OA= OB,OC= OD,∠O= 60°,∠C= 35°,则∠DAO的度数是______
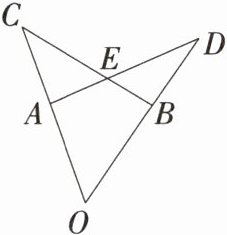
85°
.
答案:
答案 85°
解析 在△OAD和△OBC中,$\left\{\begin{array}{l} OA=OB,\\ ∠O=∠O,\\ OD=OC,\end{array}\right.$
∴△OAD≌△OBC(SAS),
∴∠D=∠C.
∵∠C=35°,
∴∠D=35°.
∴∠DAO=180° - ∠O - ∠D=180° - 60° - 35°=85°,故答案为85°.
解析 在△OAD和△OBC中,$\left\{\begin{array}{l} OA=OB,\\ ∠O=∠O,\\ OD=OC,\end{array}\right.$
∴△OAD≌△OBC(SAS),
∴∠D=∠C.
∵∠C=35°,
∴∠D=35°.
∴∠DAO=180° - ∠O - ∠D=180° - 60° - 35°=85°,故答案为85°.
6.在台风来临之前,园林管理人员用钢管加固树木(如图),树干固定点为P点,树干PO垂直于地面AB,地面固定点A,B到树干底部点O的距离相等,此时两钢管PA,PB的长度相等吗? 为什么?
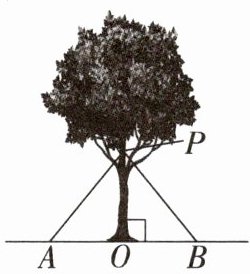
PA=PB。理由:在△POA和△POB中,$\left\{\begin{array}{l} PO=PO,\\ ∠POA=∠POB=90°,\\ AO=BO,\end{array}\right.$∴△POA≌△POB(SAS),∴PA=PB。

答案:
解析 PA=PB.
理由:在△POA和△POB中,$\left\{\begin{array}{l} PO=PO,\\ ∠POA=∠POB=90°,\\ AO=BO,\end{array}\right.$
∴△POA≌△POB(SAS),
∴PA=PB.
理由:在△POA和△POB中,$\left\{\begin{array}{l} PO=PO,\\ ∠POA=∠POB=90°,\\ AO=BO,\end{array}\right.$
∴△POA≌△POB(SAS),
∴PA=PB.
7.「2025广东韶关期末」如图,点A,D,B,F在一条直线上,AC//EF,AC= EF,AD= BF.
(1)求证:△ABC≌△FDE.
证明:∵AC//EF,
∴∠A=∠F,
∵AD=BF,
∴AD + DB=BF + DB,即AB=FD,
在△ABC和△FDE中,$\left\{\begin{array}{l} AC=EF,\\ ∠A=∠F,\\ AB=FD,\end{array}\right.$
∴△ABC≌△FDE(
(2)若∠A= 30°,∠ABC= 75°,求∠E的度数.
∵∠A=30°,∠ABC=75°,
∴∠C=180° - ∠A - ∠ABC=75°,
∵△ABC≌△FDE,
∴∠E=∠C=
(1)求证:△ABC≌△FDE.
证明:∵AC//EF,
∴∠A=∠F,
∵AD=BF,
∴AD + DB=BF + DB,即AB=FD,
在△ABC和△FDE中,$\left\{\begin{array}{l} AC=EF,\\ ∠A=∠F,\\ AB=FD,\end{array}\right.$
∴△ABC≌△FDE(
SAS
).(2)若∠A= 30°,∠ABC= 75°,求∠E的度数.
∵∠A=30°,∠ABC=75°,
∴∠C=180° - ∠A - ∠ABC=75°,
∵△ABC≌△FDE,
∴∠E=∠C=
75°
.
答案:
解析 (1)证明:
∵AC//EF,
∴∠A=∠F,
∵AD=BF,
∴AD + DB=BF + DB,即AB=FD,
在△ABC和△FDE中,$\left\{\begin{array}{l} AC=EF,\\ ∠A=∠F,\\ AB=FD,\end{array}\right.$
∴△ABC≌△FDE(SAS).
(2)
∵∠A=30°,∠ABC=75°,
∴∠C=180° - ∠A - ∠ABC=75°,
∵△ABC≌△FDE,
∴∠E=∠C=75°.
∵AC//EF,
∴∠A=∠F,
∵AD=BF,
∴AD + DB=BF + DB,即AB=FD,
在△ABC和△FDE中,$\left\{\begin{array}{l} AC=EF,\\ ∠A=∠F,\\ AB=FD,\end{array}\right.$
∴△ABC≌△FDE(SAS).
(2)
∵∠A=30°,∠ABC=75°,
∴∠C=180° - ∠A - ∠ABC=75°,
∵△ABC≌△FDE,
∴∠E=∠C=75°.
查看更多完整答案,请扫码查看


