《2025年5年中考3年模拟八年级数学上册人教版》

1. 「2025江苏南通期末」下列运算正确的是(B)
A. $ a^{3} \cdot a^{3}= a^{9} $
B. $ a^{6} ÷ a^{2}= a^{4} $
C. $ \left(a^{3}\right)^{2}= a^{5} $
D. $ (a b)^{3}= a b^{3} $

答案： B 因为 $ a ^ { 3 } \cdot a ^ { 3 } = a ^ { 6 } $，$ a ^ { 6 } \div a ^ { 2 } = a ^ { 4 } $，$ ( a ^ { 3 } ) ^ { 2 } = a ^ { 6 } $，$ ( a b ) ^ { 3 } = a ^ { 3 } b ^ { 3 } $，所以选项 A、C、D 运算均不正确，选项 B 运算正确。

2. 「2025广东湛江期末」若(2a)$ \cdot 2 a^{2} b= 4 a^{3} b $,则括号内应填的单项式是(B)
A. $ a $
B. $ 2 a $
C. $ a b $
D. $ 2 a b $

答案： B $ 4 a ^ { 3 } b \div 2 a ^ { 2 } b = 2 a $。故选 B。

3. 下列运算正确的是(D)
A. $ a^{4}+a^{3}= a^{7} $
B. $ (a-1)^{2}= a^{2}-1 $
C. $ \left(2 a^{3} b\right)^{2}= 2 a^{6} b^{2} $
D. $ a(2 a+1)= 2 a^{2}+a $

答案： D 因为 $ a ^ { 4 } $ 与 $ a ^ { 3 } $ 不能合并，所以 A 选项不符合题意；因为 $ ( a - 1 ) ^ { 2 } = a ^ { 2 } - 2 a + 1 $，所以 B 选项不符合题意；因为 $ ( 2 a ^ { 3 } b ) ^ { 2 } = 4 a ^ { 6 } b ^ { 2 } $，所以 C 选项不符合题意；因为 $ a ( 2 a + 1 ) = 2 a ^ { 2 } + a $，所以 D 选项符合题意。故选 D。

4. 下列各式不能用平方差公式计算的是(D)
A. $ (5 x-2 a b)(5 x+2 a b) $
B. $ (a x-y)(-a x-y) $
C. $ (-a b-c)(a b-c) $
D. $ (m+n)(-m-n) $

答案： D $ ( m + n ) ( - m - n ) = - ( m + n ) ( m + n ) $，不符合平方差公式的应用结构，不可以用平方差公式进行计算，故选 D。

5. 「2025云南文山州期中」数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:$ -3 x y(4 y-2 x-1)= -12 x y^{2}+6 x^{2} y+■ $,■的地方被钢笔水弄污了,你认为■处应为(A)
A. $ 3 x y $
B. $ -3 x y $
C. $ -1 $
D. $ 1 $

答案： A $ \because - 3 x y ( 4 y - 2 x - 1 ) = - 12 x y ^ { 2 } + 6 x ^ { 2 } y + 3 x y = - 12 x y ^ { 2 } + 6 x ^ { 2 } y + \blacksquare $，$ \therefore \blacksquare $ 处应为 $ 3 x y $。故选 A。

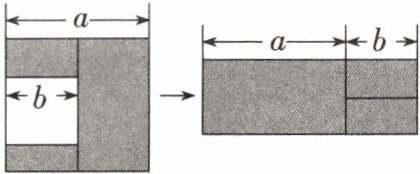
6. 如图,在边长为$ a 的正方形中挖掉一个边长为 b $的小正方形,把余下的部分拼成一个长方形(无重叠部分),通过计算两个图形中阴影部分的面积,可以验证的一个等式是(A)

A. $ (a+b)(a-b)= a^{2}-b^{2} $
B. $ a(a-b)= a^{2}-a b $
C. $ (a-b)^{2}= a^{2}-2 a b+b^{2} $
D. $ a(a+b)= a^{2}+a b $

答案： A 根据图形可知第一个图形阴影部分的面积为 $ a ^ { 2 } - b ^ { 2 } $，第二个图形阴影部分的面积为 $ ( a + b ) ( a - b ) $，即 $ ( a + b ) ( a - b ) = a ^ { 2 } - b ^ { 2 } $，故选 A。

7. 若$ 3^{x}= 5,3^{y}= 4,3^{2 z}= 2 $,则$ 3^{2 x-y+4 z} $的值为(D)
A. $ \frac{25}{4} $
B. $ 10 $
C. $ 20 $
D. $ 25 $

答案： D 因为 $ 3 ^ { x } = 5 $，$ 3 ^ { y } = 4 $，$ 3 ^ { 2 z } = 2 $，所以 $ 3 ^ { 2 x - y + 4 z } = ( 3 ^ { x } ) ^ { 2 } \div 3 ^ { y } \times ( 3 ^ { 2 z } ) ^ { 2 } = 25 \div 4 \times 4 = 25 $。故选 D。

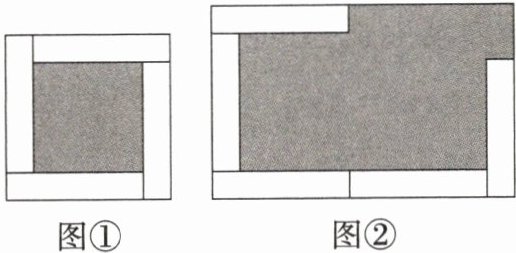
8. 图①是由4个全等的白色的长方形和1个灰色的正方形构成的正方形,图②是由5个全等的白色的长方形(每个长方形的大小和图①相同)和1个灰色的不规则图形构成的长方形.已知图①②中灰色图形的面积分别为35和102,则每个白色长方形的面积为(8)

A. $ 32 $
B. $ 16 $
C. $ 8 $
D. $ 2 $

答案： C 设每个白色长方形的长为 $ a $，宽为 $ b $，由题图①可得 $ ( a + b ) ^ { 2 } - 4 a b = 35 $，即 $ a ^ { 2 } + b ^ { 2 } = 2 a b + 35 $，由题图②可得 $ ( 2 a + b ) ( a + 2 b ) - 5 a b = 102 $，即 $ a ^ { 2 } + b ^ { 2 } = 51 $，$ \therefore 2 a b + 35 = 51 $，$ \therefore a b = 8 $，故每个白色长方形的面积为 8。

9. 「2025河北衡水月考」若$ \left(\frac{1}{3} x-6 y\right)^{2}= \frac{1}{9} x^{2}-4 x y+k^{2} y^{2} $,则$ k $的值为______±6.

答案： 答案 $ \pm 6 $
解析 $ \because \left( \frac { 1 } { 3 } x - 6 y \right) ^ { 2 } = \frac { 1 } { 9 } x ^ { 2 } - 4 x y + 36 y ^ { 2 } $，$ \therefore k ^ { 2 } = 36 $，$ \therefore k = \pm 6 $。故答案为 $ \pm 6 $。

10. 「2025上海宝山期末」如果$ 8 x^{4} y^{a} ÷\left(-2 x^{b} y^{3}\right)^{2}= 2 y $,那么$ a^{b}= $______49.

答案： 答案 49
解析 $ \because 8 x ^ { 4 } y ^ { a } \div ( - 2 x ^ { b } y ^ { 3 } ) ^ { 2 } = 2 y $，$ \therefore 8 x ^ { 4 } y ^ { a } \div 4 x ^ { 2 b } y ^ { 6 } = 2 y $，$ \therefore 2 x ^ { 4 - 2 b } y ^ { a - 6 } = 2 y $，$ \therefore 4 - 2 b = 0 $，$ a - 6 = 1 $，$ \therefore b = 2 $，$ a = 7 $，$ \therefore a ^ { b } = 7 ^ { 2 } = 49 $，故答案为 49。

11. 「2025四川眉山期中」若$ m-n= 4, m n= -3 $,则$ \left(m^{2}-4\right)\left(n^{2}-4\right) $的值为______-15.

答案： 答案 -15
解析 $ \because m - n = 4 $，$ m n = - 3 $，$ \therefore m ^ { 2 } + n ^ { 2 } = ( m - n ) ^ { 2 } + 2 m n = 4 ^ { 2 } + 2 \times ( - 3 ) = 16 - 6 = 10 $，$ \therefore ( m ^ { 2 } - 4 ) ( n ^ { 2 } - 4 ) = m ^ { 2 } n ^ { 2 } - 4 ( m ^ { 2 } + n ^ { 2 } ) + 16 = ( - 3 ) ^ { 2 } - 4 \times 10 + 16 = 9 - 40 + 16 = - 15 $，故答案为 -15。

12. 若$ \left(x^{2}-2 x-3\right)\left(x^{3}+5 x^{2}-6 x+7\right)= a_{5} x^{5}+a_{4} x^{4}+a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0} $,则$ a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+a_{5}= $______-28.

答案： 答案 -28
解析 【解法一】$ \because ( x ^ { 2 } - 2 x - 3 ) ( x ^ { 3 } + 5 x ^ { 2 } - 6 x + 7 ) = x ^ { 5 } + 5 x ^ { 4 } - 6 x ^ { 3 } + 7 x ^ { 2 } - 2 x ^ { 4 } - 10 x ^ { 3 } + 12 x ^ { 2 } - 14 x - 3 x ^ { 3 } - 15 x ^ { 2 } + 18 x - 21 = x ^ { 5 } + 3 x ^ { 4 } - 19 x ^ { 3 } + 4 x ^ { 2 } + 4 x - 21 = a _ { 5 } x ^ { 5 } + a _ { 4 } x ^ { 4 } + a _ { 3 } x ^ { 3 } + a _ { 2 } x ^ { 2 } + a _ { 1 } x + a _ { 0 } $，$ \therefore a _ { 0 } = - 21 $，$ a _ { 1 } = 4 $，$ a _ { 2 } = 4 $，$ a _ { 3 } = - 19 $，$ a _ { 4 } = 3 $，$ a _ { 5 } = 1 $，$ \therefore a _ { 0 } + a _ { 1 } + a _ { 2 } + a _ { 3 } + a _ { 4 } + a _ { 5 } = - 21 + 4 + 4 - 19 + 3 + 1 = - 28 $。【解法二】当 $ x = 1 $ 时，$ a _ { 5 } + a _ { 4 } + a _ { 3 } + a _ { 2 } + a _ { 1 } + a _ { 0 } = ( 1 - 2 - 3 ) \times ( 1 + 5 - 6 + 7 ) = - 4 \times 7 = - 28 $。