《2025年一线调研学业测评八年级数学下册北师大版》

1. 下列运动属于旋转的是（ ）
A. 滚动过程中的篮球的滚动
B. 钟表的钟摆的摆动
C. 气球升空的运动
D. 一个图形沿某直线对折的过程

答案： B

2. 如图，将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后，得到的图形为（ ）

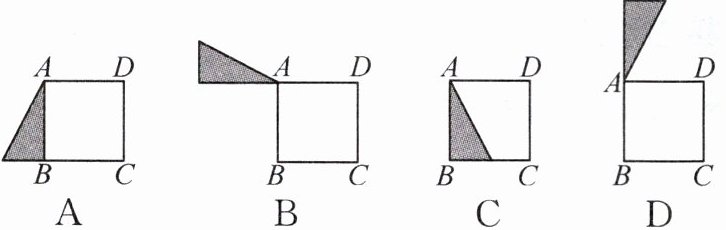
答案： A

3. 将一图形绕着点O顺时针方向旋转60°，再绕着点O逆时针方向旋转170°，这时如果使图形回到原来的位置，需要将图形绕着点O（ ）
A. 顺时针旋转230°
B. 逆时针旋转110°
C. 顺时针旋转110°
D. 逆时针旋转230°

答案： C

4. 如图，将Rt△ABC（其中∠B = 34°，∠C = 90°）绕点A按顺时针方向旋转到△AB₁C₁的位置，使得点C，A，B₁在同一条直线上，那么旋转角等于（ ）

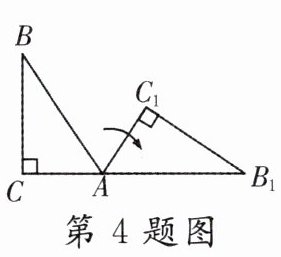
A. 34°
B. 56°
C. 124°
D. 145°

答案： C

5. 如图，在Rt△ABC中，∠B = 90°，BC = 6，AB = 8. 将△ABC绕点A顺时针旋转90°得到△AB′C′，连接CC′，则CC′的长为（ ）

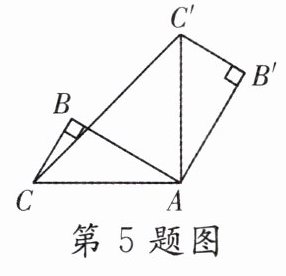
A. 10√2
B. 20
C. 10
D. 3√26

答案： A

6. 如图，△ABC中，∠CAB = 72°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得C′C//AB，则∠AB′B的度数为（ ）

A. 34°
B. 36°
C. 72°
D. 46°

答案： C

7. 如图，已知线段MN = 4，点A在线段MN上，且AM = 1，点B为线段AN上的一个动点. 以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，旋转角分别为α和β. 若旋转后M，N两点重合成一点（即构成△ABC）. 设AB = x.
（1）△ABC的周长为____.
（2）若α + β = 270°，求x的值.

答案： 解:
(1)4　提示:由旋转性质，得$AM = AC = 1$，$BN = BC = 3 - x$.$\therefore\triangle ABC$的周长为$AC + AB + BC = MN = 4$.
(2)$\because\alpha+\beta = 270^{\circ}$，$\therefore\angle CAB+\angle CBA = 360^{\circ}-270^{\circ}=90^{\circ}$.$\therefore\angle ACB = 180^{\circ}-(\angle CAB+\angle CBA)=180^{\circ}-90^{\circ}=90^{\circ}$.$\therefore AC^{2}+BC^{2}=AB^{2}$，即$1^{2}+(3 - x)^{2}=x^{2}$. 解得$x=\frac{5}{3}$.

8. (广安中考)如图，将△ABC绕点A逆时针旋转55°得到△ADE，若∠E = 70°且AD⊥BC于点F，则∠BAC的度数为（ ）

A. 65°
B. 70°
C. 75°
D. 80°

答案： C