《2025年一线调研学业测评八年级数学下册北师大版》

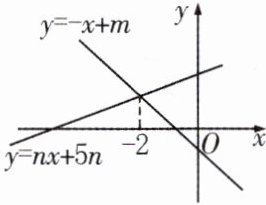
10. 如图，直线$y = -x + m$与直线$y = nx + 5n$（$n\neq0$）的交点横坐标为 -2，则关于$x$的不等式$-x + m\gt nx + 5n\gt0$的整数解为（ ）

A. -5，-4，-3
B. -4，-3
C. -4，-3，-2
D. -3，-2

答案： B

11. 某化工厂库存 A 种原料 52 千克，B 种原料 64 千克，现用这些原料生产甲、乙两种产品共 20 件. 已知生产 1 件甲种产品需要 A 种原料 3 千克，B 种原料 2 千克；生产 1 件乙种产品需要 A 种原料 2 千克，B 种原料 4 千克. 则有_____种生产方案.

答案： 5 【解析】设生产甲种产品$x$件，则生产乙种产品$(20 - x)$件. 根据题意，得$\begin{cases}3x + 2(20 - x)\leqslant 52\\2x + 4(20 - x)\leqslant 64\end{cases}$，解得$8\leqslant x\leqslant 12$. 又$\because x$为整数，$\therefore x = 8,9,10,11,12$. $\therefore$有 5 种生产方案.

12. 若$a$，$b$，$c$是$\triangle ABC$的三边长，且$a$，$b$满足$|a - 6| + (b - 8)^2 = 0$，$c$是不等式组$\begin{cases}\frac{2x + 5}{4}\gt x - 4 \\ 3(x + 2)\lt4x + 1\end{cases}$的最大整数解，求$\triangle ABC$的周长.

答案： 解：$\because |a - 6|+(b - 8)^2 = 0$，$\therefore a = 6,b = 8$.
由不等式组$\begin{cases}\frac{2x + 5}{4} ＞ x - 4\\3(x + 2) ＜ 4x + 1\end{cases}$，解得$5 ＜ x ＜ 10\frac{1}{2}$.
$\therefore c = 10$. $\therefore\triangle ABC$的周长为$6 + 8 + 10 = 24$.

13. 九(2)班计划购买 A，B 两种相册共 42 册作为毕业礼品，已知 A 种相册的单价比 B 种的多 10 元，买 4 册 A 种相册与买 5 册 B 种相册的费用相同.
(1)求 A，B 两种相册的单价分别是多少元？
(2)由于学生对两类相册喜好不同，经调查得知，购买的 A 种相册的数量要少于 B 种相册数量的$\frac{3}{4}$，但又不少于 B 种相册数量的$\frac{2}{5}$. 设买 A 种相册$x$册.
①有多少种不同的购买方案？
②商店为了促销，决定对 A 种相册每册让利$a$元销售（$12\leqslant a\leqslant18$），B 种相册每册让利$b$元销售，最后班委会同学在付款时发现：购买所需的总费用与购买的方案无关，当总费用最少时，求此时$a$的值.

答案： 解：
(1)设A种相册的单价为$m$元，B种相册的单价为$n$元，依题意，得$\begin{cases}m - n = 10\\4m = 5n\end{cases}$，解得$\begin{cases}m = 50\\n = 40\end{cases}$.
故A种相册的单价为 50 元，B种相册的单价为 40 元.
(2)①依题意，得$\begin{cases}x ＜ \frac{3}{4}(42 - x)\\x\geqslant \frac{2}{5}(42 - x)\end{cases}$，解得$12\leqslant x ＜ 18$.
又$\because x$为正整数，$\therefore x$可取$12,13,14,15,16,17$，共 6 种不同的购买方案.
②设购买总费用为$w$元，依题意，得$w=(50 - a)x+(40 - b)(42 - x)=(10 - a + b)x + 42(40 - b)$.
$\because$购买所需的总费用与购买的方案无关，则$w$的值与$x$无关，$\therefore 10 - a + b = 0$. $\therefore b = a - 10$.
$\therefore w = 42(40 - b)=42[40 - (a - 10)]=-42a + 2100$.
$\because -42 ＜ 0$，$\therefore w$随$a$的增大而减小.
又$\because 12\leqslant a\leqslant 18$，$\therefore$当$a = 18$时，$w$取得最小值.
答：当总费用最少时，$a$的值为 18.