《2025年一线调研学业测评八年级数学下册北师大版》

1. 下列各式由左到右的变形中，属于分解因式的是 （ ）
A. $a(m + n)=am + an$
B. $a^{2}-b^{2}-c^{2}=(a - b)(a + b)-c^{2}$
C. $10x^{2}-15x = 5x(2x - 3)$
D. $x^{2}-16 + 6x=(x + 4)(x - 4)+6x$

答案： C

2. 若多项式$x^{2}+ax - 28$分解因式为$(x - 4)(x + 7)$，则$a$的值是 （ ）
A. $-11$
B. $-3$
C. $3$
D. $11$

答案： C

3. $(x + 3)(2x - 1)$是多项式________因式分解的结果.

答案： $2x^{2}+5x - 3$

4. 计算$19.97×85 + 19.97×15$的最简方法是 （ ）
A. $19.97×85 + 19.97×15 = 19.97×(85 + 15)$
B. $19.97×85 + 19.97×15 = 5×(19.97×17 + 19.97×3)$
C. $19.97×85 + 19.97×15 = 1697.45 + 299.55$
D. $19.97×85 + 19.97×15 = 19.97×5×(17 + 3)$

答案： A

5. 如图，边长为$(m + 3)$的正方形纸片剪去一个边长为$m$的正方形之后，余下部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为$3$，则此长方形的周长是 （ ）

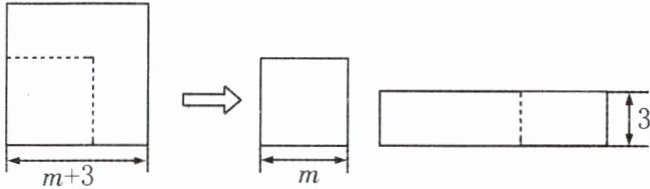
A. $2m + 6$
B. $4m + 6$
C. $4m + 12$
D. $2m + 12$

答案： C

6. 已知多项式$x + 81b^{4}$可以分解为$(4a^{2}+9b^{2})(2a + 3b)(3b - 2a)$，则$x$的值是（ ）
A. $16a^{4}$
B. $-16a^{4}$
C. $4a^{2}$
D. $-4a^{2}$

答案： B [解析]$(4a^{2}+9b^{2})(2a + 3b)(3b - 2a)=-(4a^{2}+9b^{2})(2a + 3b)(2a - 3b)=-(4a^{2}+9b^{2})(4a^{2}-9b^{2})=-(16a^{4}-81b^{4})=-16a^{4}+81b^{4}$. 故可得$x$的值是$-16a^{4}$.

7. 图中的四边形均为长方形，根据图形的面积关系，写出一个有关多项式因式分解的等式：________________________.

答案： $ma+mb+mc+na+nb+nc=(m + n)(a + b + c)$

8. 仔细阅读下面例题，解答问题：
例题：已知二次三项式$x^{2}-4x + m$有一个因式是$(x + 3)$，求另一个因式以及$m$的值.
解：设另一个因式为$(x + n)$，
由题意得$x^{2}-4x + m=(x + 3)(x + n)$，即$x^{2}-4x + m=x^{2}+(n + 3)x + 3n$. $\therefore n + 3=-4$，$3n = m$. 解得$n=-7$，$m=-21$.
$\therefore$另一个因式为$(x - 7)$，$m$的值为$-21$.
问题：
（1）若二次三项式$x^{2}-5x + 6$可分解为$(x - 2)(x + a)$，则$a=$________.
（2）若二次三项式$2x^{2}+bx - 5$可分解为$(2x - 1)(x + 5)$，则$b=$________.

答案：
(1)$-3$　
(2)$9$