第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图,直径为2cm的圆$O_1$平移3cm到圆$O_2$,则图中阴影部分的面积为______$cm^2$.
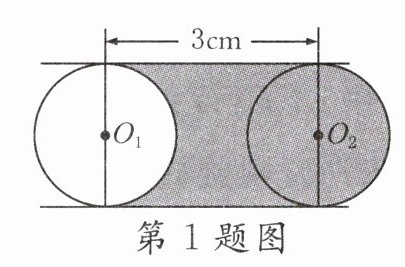

答案:
6
2. 如图,O为坐标原点,$\triangle OAB$是等腰直角三角形,$\angle OAB = 90^{\circ}$,点B的坐标为$(0,2\sqrt{2})$,将该三角形沿x轴向右平移得到$Rt\triangle O'A'B'$,此时点$B'$的坐标为$(2\sqrt{2},2\sqrt{2})$,则线段OA在平移过程中扫过部分的图形面积为______.
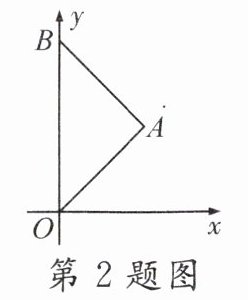

答案:
4 【解析】由平移的性质,得$AA' = BB' = 2\sqrt{2}$.
$\because\triangle OAB$是等腰直角三角形,$\therefore$点$A$的坐标为$(\sqrt{2},\sqrt{2})$.$\therefore$线段$OA$在平移过程中扫过部分的图形面积为$2\sqrt{2}\times\sqrt{2}=4$.
$\because\triangle OAB$是等腰直角三角形,$\therefore$点$A$的坐标为$(\sqrt{2},\sqrt{2})$.$\therefore$线段$OA$在平移过程中扫过部分的图形面积为$2\sqrt{2}\times\sqrt{2}=4$.
3. 如图,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路,宽均为1米,其他部分均种植花草. 试求出种植花草的面积.
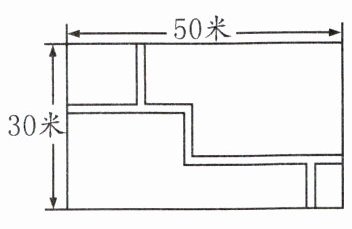

答案:
解:根据题意,得种植花草的面积$=(50 - 1)\times(30 - 1)=1421$(平方米). 故种植花草的面积是 1421 平方米.
4. 如图,将直角梯形ABCD平移得到直角梯形EFGH,若$HG = 10$,$MC = 2$,$MG = 3$,求图中阴影部分的面积.
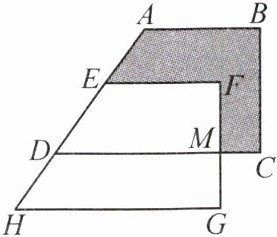

答案:
解:由平移的性质,得$S_{梯形ABCD}=S_{梯形EFGH}$.$\therefore S_{阴影}=S_{梯形ABCD}-S_{梯形EFMD}=S_{梯形EFGH}-S_{梯形EFMD}$.$\therefore S_{阴影}=S_{梯形DHGM}$.$\because DC = HG = 10$,$MC = 2$,$MG = 3$,且梯形$EFGH$为直角梯形,$\therefore S_{阴影}=S_{梯形DHGM}=\frac{1}{2}\times(10 - 2 + 10)\times3 = 27$.
5. 如图,在$\triangle ABC$中,$AB = 4$,$BC = 6$,$\angle B = 60^{\circ}$,将$\triangle ABC$沿射线BC的方向平移2个单位长度后,得到$\triangle A'B'C'$,连接$A'C$,则$\triangle A'B'C$的周长为______.
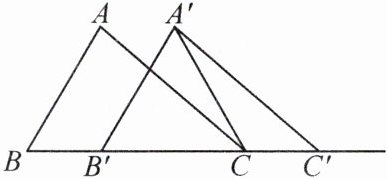

答案:
12
6. 如图,在$Rt\triangle ABC$中,$AC = 5$,$BC = 12$,求内部五个小直角三角形的周长.
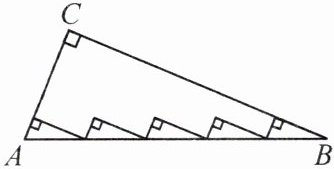

答案:
解:由图形可以看出内部小三角形的直角边可由$Rt\triangle ABC$的直角边平移得到,在$Rt\triangle ABC$中,$AC = 5$,$BC = 12$,$\therefore AB = 13$.$\therefore$内部五个小直角三角形的周长为$AC + BC + AB = 30$.
7. 如图,已知$\triangle ABC$的面积为36,将$\triangle ABC$沿BC平移得到$\triangle A'B'C'$,使点$B'$和点C重合,连接$AC'$交$A'C$于点D.
(1)求证:$A'D = CD$.
(2)求$\triangle C'DC$的面积.
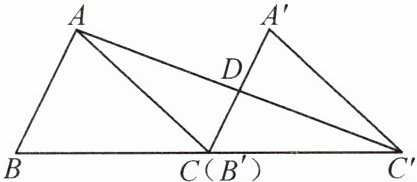
(1)求证:$A'D = CD$.
(2)求$\triangle C'DC$的面积.

答案:
(1)证明:$\because\triangle ABC$沿$BC$平移得到$\triangle A'B'C'$,
$\therefore AC// A'C'$,$AC = C'A'$.$\therefore\angle ACD=\angle C'A'D$.
又$\because\angle ADC=\angle C'DA'$,$\therefore\triangle ACD\cong\triangle C'A'D$.
$\therefore CD = A'D$,即$A'D = CD$.
(2)解:$\because\triangle ABC$沿$BC$平移得到$\triangle A'B'C'$,$\therefore\triangle ABC\cong\triangle A'B'C'$.$\therefore S_{\triangle ABC}=S_{\triangle A'B'C'}=36$.$\because A'D = CD$,
$\therefore S_{\triangle CDC'}=S_{\triangle C'A'D}=\frac{1}{2}S_{\triangle A'B'C'}=18$.
(1)证明:$\because\triangle ABC$沿$BC$平移得到$\triangle A'B'C'$,
$\therefore AC// A'C'$,$AC = C'A'$.$\therefore\angle ACD=\angle C'A'D$.
又$\because\angle ADC=\angle C'DA'$,$\therefore\triangle ACD\cong\triangle C'A'D$.
$\therefore CD = A'D$,即$A'D = CD$.
(2)解:$\because\triangle ABC$沿$BC$平移得到$\triangle A'B'C'$,$\therefore\triangle ABC\cong\triangle A'B'C'$.$\therefore S_{\triangle ABC}=S_{\triangle A'B'C'}=36$.$\because A'D = CD$,
$\therefore S_{\triangle CDC'}=S_{\triangle C'A'D}=\frac{1}{2}S_{\triangle A'B'C'}=18$.
查看更多完整答案,请扫码查看


