《2025年一线调研学业测评八年级数学下册北师大版》

1. 如图所示，点P为△ABC三边的垂直平分线的交点，PA = 6，则点P到点C的距离为PC满足（ ）

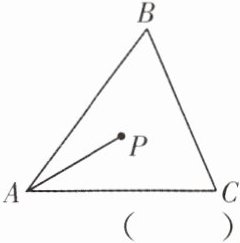
A. PC＜6
B. PC = 6
C. PC＞6
D. 以上都不对

答案： B

2. 如图，某市的三个城镇中心A，B，C构成△ABC，该市政府打算修建一个大型体育中心P，使得该体育中心到三个城镇中心A，B，C的距离相等，则P点应设计在（ ）

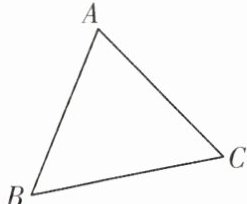
A. 三个角的角平分线的交点上
B. 三角形三条高的交点上
C. 三条边的垂直平分线的交点上
D. 三角形三条中线的交点上

答案： C

3. 如图，在△ABC中，DE，DF分别为BC，AB边的垂直平分线，连接AD，CD.
（1）若∠B = 40°，求∠ACD的度数.
（2）直接写出∠B与∠ACD之间的数量关系：________________.

答案：
解:
(1)连接BD并延长，交AC于点H,
∵DE,DF分别为BC,AB边的垂直平分线，
∴DA=DB,DC=DB.
∴∠DAB=∠DBA,∠DCB=∠DBC.
∴∠ADH=∠DAB+∠DBA=2∠DBA,∠CDH=∠DCB+∠DBC=2∠DBC.
∴∠ADC=2∠ABC=80°.
∵DA=DB,DC=DB,
∴DA=DC.
∴∠ACD=∠CAD=$\frac{1}{2}$×(180°−80°)=50°.
　　　　　　　　　　　　　　　　
(2)∠B+∠ACD=90°

4. 下列尺规作图，能判断AD是△ABC边上的中线的是（ ）

答案： A

5. （阿坝州中考）如图，在△ABC中，∠BAC = 70°，∠C = 40°，分别以点A和点C为圆心、大于$\frac{1}{2}AC$的长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD，则∠BAD的大小为（ ）

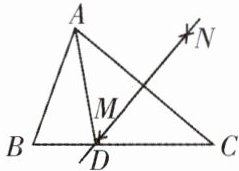
A. 30°
B. 40°
C. 50°
D. 60°

答案： A

6. 如图，线段AB，BC的垂直平分线$l_1$，$l_2$相交于点O. 若∠OEB = 46°，则∠AOC的大小为（ ）

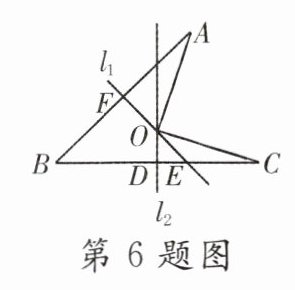
A. 92°
B. 88°
C. 46°
D. 86°

答案： B

7. 如图，边长为3的等边三角形ABC内一点O到三个顶点的距离都相等，则OA = ______.

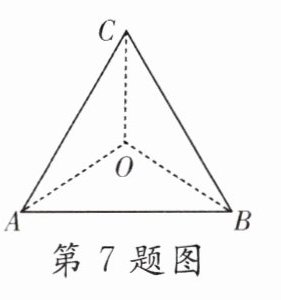
答案： $\sqrt{3}$

8. 如图，在△ABC中，AB = AC = 5，BC = 6，AD平分∠BAC交BC于点D，分别以点A，C为圆心、大于$\frac{1}{2}AC$长为半径作弧，两弧相交于点M和点N，作直线MN，交AD于点P，则DP的长为（ ）

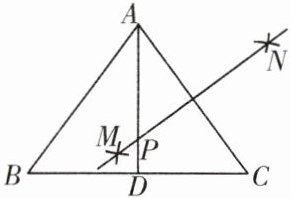
A. $\frac{3}{8}$
B. $\frac{5}{8}$
C. $\frac{7}{8}$
D. 1

答案：
C 【解析】由作法得MN垂直平分AC，连接PC,
∴PA =PC.
∵AB=AC=5,AD平分∠BAC交BC于点D,
∴AD⊥BC,BD=CD=$\frac{1}{2}$BC=3.在Rt△ABD中,AD=$\sqrt{AB^{2}-BD^{2}}$=$\sqrt{5^{2}-3^{2}}$=4,设PD=x,则PA =PC=4−x,在Rt△PCD中,x²+3²=(4−x)²,解得x=$\frac{7}{8}$,即DP的长为$\frac{7}{8}$.