《2025年一线调研学业测评八年级数学下册北师大版》

1. 若$x＜y$，则$x + 2$______$y + 2$.

答案： ＜

2. 已知数$a$，$b$的对应点在数轴上的位置如图所示，则$a - 3$______$b - 3$.

答案： ＜

3. 若$3x＞-3y$，则下列不等式中一定成立的是（ ）
A. $x＞-y$
B. $x＞y$
C. $x＜-y$
D. $x＜y$

答案： A

4. 若$x＜y$，试比较大小：$2x - 6$______$2y - 6$.

答案： ＜

5. 将下列不等式化成“$x＞a$”或“$x＜a$”的形式：
（1）$2x + 5＞3$； （2）$10x - 1＞7x$.

答案：
(1)$x ＞ -1$　
(2)$x ＞ \frac{1}{3}$

6. 若$a＜0$，则下列不等式中不成立的是（ ）

A. $3a＜2a$
B. $a - 3＜a - 2$
C. $-3a＞-2a$
D. $a＞-\frac{a}{2}$

答案： D

7. 下列不等式变形正确的是（ ）
A. 由$a＞b$得$ac＞bc$
B. 由$a＞b$得$-2a＞-2b$
C. 由$a＞b$得$-a＜-b$
D. 由$a＞b$得$a - 2＜b - 2$

答案： C

8. 已知$x＞y$，则$-\frac{1}{2}x$______$-\frac{1}{2}y$.

答案： ＜

10. 将下列不等式化成“$x＞a$”或“$x＜a$”的形式：
（1）$-\frac{1}{2}x＞-1$； （2）$-6(x - 1)＜0$.

答案：
(1)$x ＜ 2$　
(2)$x ＞ 1$

11. 若$m＜n$，且$(a - 5)m＞(a - 5)n$，求$a$的取值范围.

答案： 解：$\because m ＜ n$，且$(a - 5)m ＞ (a - 5)n$，
$\therefore a - 5 ＜ 0$，解得$a ＜ 5$。

12. 设“●”“▲”“■”表示三种不同的物体，现用天平称了两次，情况如图所示，那么这三种物体按质量从大到小的顺序排列应为（ ）

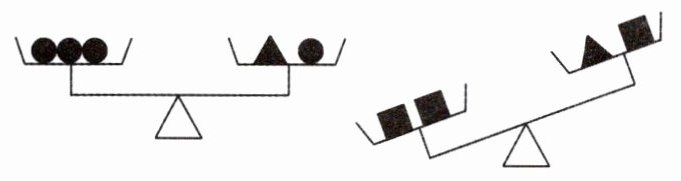
A. ●、▲、■
B. ■、▲、●
C. ▲、■、●
D. ■、●、▲

答案： B

13. 若实数$a$，$b$，$c$在数轴上对应点的位置如图所示，则下列不等式成立的是（ ）

A. $a - c＞b - c$
B. $a + c＜b + c$
C. $ac＞bc$
D. $\frac{a}{6}＜\frac{c}{6}$

答案： B