《2025年一线调研学业测评八年级数学下册北师大版》

1. 在式子$-\frac{1}{a},\frac{b}{3},\frac{c}{a - b},\frac{2ab}{\pi},\frac{x}{x^{2}-y^{2}}$中，分式的个数为（ ）
A. 2
B. 3
C. 4
D. 5

答案： B

2. 若分式$\frac{1}{x + 2}$在实数范围内有意义，则实数$x$的取值范围是（ ）
A. $x ＞ - 2$
B. $x ＜ - 2$
C. $x = - 2$
D. $x\neq - 2$

答案： D

3. 下列各式中，不论字母取何值时分式都有意义的是（ ）
A. $\frac{1}{2x + 1}$
B. $\frac{1}{2x - 1}$
C. $\frac{1 - 3x}{x^{2}}$
D. $\frac{5x + 3}{2x^{2}+1}$

答案： D

4. 若$x = - 2$，则分式$\frac{x - 4}{1 - x}$的值是（ ）
A. 2
B. - 2
C. - 6
D. 无意义

答案： B

5. 若分式$\frac{2x - 2}{x^{2}+1}$的值是负数，则$x$的取值范围是（ ）

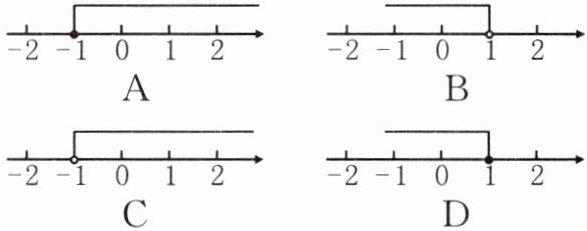
答案： B

6. 若分式$\frac{3-\vert x\vert}{x + 3}$的值为零，则$x$的值是（ ）
A. 3
B. - 3
C. $\pm3$
D. 0

答案： A

7. 甲、乙两地相距5千米，汽车从甲地到乙地，速度为$v$千米/时，可按时到达. 若每时多行驶$a$千米，则汽车提前__________时到达.

答案： $(\frac{5}{v}-\frac{5}{v + a})$

8. 若$a^{2}-ab = 0(b\neq0)$，则$\frac{a}{a + b}=$（ ）
A. 0
B. $\frac{1}{2}$
C. 0或$\frac{1}{2}$
D. 1或2

答案： C

9. 如图，一个瓶身为圆柱体的玻璃瓶内装有高$a$厘米的墨水，将瓶盖盖好后倒置，墨水水面高为$h$厘米，则瓶内的墨水的体积约占玻璃瓶容积的（ ）

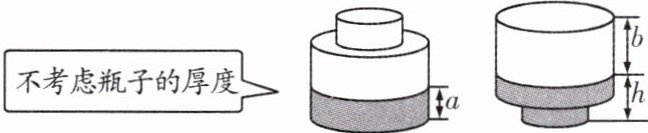
A. $\frac{a}{a + b}$
B. $\frac{b}{a + b}$
C. $\frac{h}{a + b}$
D. $\frac{h}{a + h}$

答案： A

10. 已知$a:b:c = 2:3:5$，求分式$\frac{a - 3b + 2c}{b - c}$的值.

答案： 解：$\because a:b:c = 2:3:5$，$\therefore$设$a = 2k$，$b = 3k$，$c = 5k(k\neq0)$，$\therefore\frac{a - 3b + 2c}{b - c}=\frac{2k - 9k + 10k}{3k - 5k}=-\frac{3}{2}$，即分式$\frac{a - 3b + 2c}{b - c}$的值是$-\frac{3}{2}$。

11. 不论$x$取何实数，分式$\frac{1}{x^{2}-2x + m}$总有意义，求$m$的取值范围.

答案： 解：由题意可知，当$x^{2}-2x + m\neq0$时，分式有意义。$\therefore x^{2}-2x + 1 + m - 1=(x - 1)^{2}+m - 1\neq0$。$\because(x - 1)^{2}\geq0$，$\therefore$当$m - 1＞0$，即$m＞1$时，不论$x$取何实数，分式$\frac{1}{x^{2}-2x + m}$总有意义。