《2025年一线调研学业测评八年级数学下册北师大版》

1. 利用因式分解简便计算：$2021^{2}-2021×4044 + 2022^{2}=$____.

答案： 1

2. 通过因式分解进行简便计算：$\frac{1 + 2}{1^{2}-2^{2}}+\frac{2 + 3}{2^{2}-3^{2}}+\cdots+\frac{999 + 1000}{999^{2}-1000^{2}}$.

答案： 解：$\frac{1 + 2}{1^{2}-2^{2}}+\frac{2 + 3}{2^{2}-3^{2}}+\cdots+\frac{999 + 1000}{999^{2}-1000^{2}}=\frac{1 + 2}{(1 + 2)\times(1 - 2)}+\frac{2 + 3}{(2 + 3)\times(2 - 3)}+\cdots+\frac{999 + 1000}{(999 + 1000)\times(999 - 1000)}=(-1)+(-1)+\cdots+(-1)= - 999$.

3. 已知$x + y = 0.2$，$x + 3y = 1$，则代数式$x^{2}+4xy + 4y^{2}$的值为_______.

答案： 0.36 【解析】$\because x + y = 0.2,x + 3y = 1,\therefore$两式相加得$2x+4y = 1.2$，即$x + 2y = 0.6$. 故原式$=(x + 2y)^{2}=0.36$.

4. 若$2a^{2}+6ab + 9b^{2}-2a + 1 = 0$，求$a^{2}b + 3ab^{2}$的值.

答案： 解：$\because 2a^{2}+6ab + 9b^{2}-2a + 1 = 0,\therefore(a + 3b)^{2}+(a - 1)^{2}=0.\therefore a + 3b = 0,a - 1 = 0.\therefore a^{2}b + 3ab^{2}=ab(a + 3b)=ab\times0 = 0$.

5. 对于任意自然数$n$，$(n + 7)^{2}-(n - 3)^{2}$是否能被 20 整除？

答案： 解：$(n + 7)^{2}-(n - 3)^{2}=[(n + 7)+(n - 3)][(n + 7)-(n - 3)]=(n + 7 + n - 3)(n + 7 - n + 3)=(2n + 4)\times10=20(n + 2).\because 20(n + 2)$中含有 20 这个因数，$\therefore(n + 7)^{2}-(n - 3)^{2}$能被 20 整除.

6. 若$A = x^{2}+4xy + y^{2}-4$，$B = 4x + 4xy - 6y - 25$，比较$A$，$B$的大小关系.

答案： 解：$\because A = x^{2}+4xy + y^{2}-4,B = 4x + 4xy-6y-25$，
$\therefore A - B=(x^{2}+4xy + y^{2}-4)-(4x + 4xy-6y-25)=x^{2}+y^{2}-4x + 6y + 21=(x - 2)^{2}+(y + 3)^{2}+8.\because(x - 2)^{2}+(y + 3)^{2}+8\geqslant8＞0,\therefore A - B＞0.\therefore A,B$的大小关系为$A＞B$.

7. 请阅读下列解题过程：
已知$a$，$b$，$c$为$\triangle ABC$的三边，且满足$a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4}$，试判断$\triangle ABC$的形状.
解：$\because a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4}$， ①
$\therefore c^{2}(a^{2}-b^{2})=(a^{2}+b^{2})(a^{2}-b^{2})$. ②
$\therefore c^{2}=a^{2}+b^{2}$. ③
$\therefore \triangle ABC$为直角三角形. ④
问：
(1)在上述解题过程中，从第______步开始出现错误.
(2)错误的原因是______________________________.
(3)本题正确的结论是$\triangle ABC$为____________________，请写出你认为正确的解答过程.

答案： 解：
(1)③
(2)方程两边同时除以$(a^{2}-b^{2})$，而$(a^{2}-b^{2})$的值可能是 0
(3)直角三角形或等腰三角形
$\because a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4},\therefore c^{2}(a^{2}-b^{2})=(a^{2}+b^{2})(a^{2}-b^{2}).\therefore(c^{2}-a^{2}-b^{2})(a^{2}-b^{2})=0.\therefore c^{2}=a^{2}+b^{2}$或$a^{2}=b^{2}$，即$c^{2}=a^{2}+b^{2}$或$a = b.\therefore\triangle ABC$为直角三角形或等腰三角形.

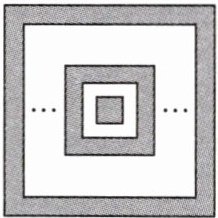
8. 如图，101 个正方形由小到大套在一起，从外向里相间地画上阴影，最外层画上阴影，最里面的一层画上阴影，最外面的正方形的边长为 101cm，向里依次为 100cm，99cm，…，1cm，那么在这个图形中，所有阴影部分的面积之和为多少？

答案： 解：$S_{阴影}=(101^{2}-100^{2})+(99^{2}-98^{2})+\cdots+(3^{2}-2^{2})+1^{2}=101 + 100 + 99 + 98+\cdots+3 + 2 + 1 = 5151(cm^{2})$. 故所有阴影部分的面积之和为$5151cm^{2}$.