《2025年一线调研学业测评八年级数学下册北师大版》

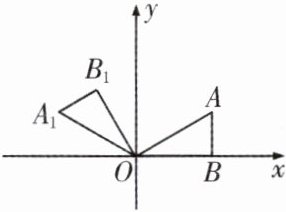
8. 如图，△ABO中，AB⊥OB，OB = $\sqrt{3}$，AB = 1，把△ABO绕点O逆时针旋转120°后得到△A₁B₁O，求点B₁的坐标.

答案：
解：过 B₁作 B₁C⊥y 轴于 C，
∵把△ABO 绕点 O 逆时针旋转 120°后得到△A₁B₁O，
∴∠BOB₁ = 120°，OB₁ = OB = $\sqrt{3}$.
∵∠BOC = 90°，
∴∠COB₁ = 30°.
∴$B_{1}C=\frac{1}{2}OB_{1}=\frac{\sqrt{3}}{2}$，$OC=\sqrt{OB_{1}^{2}-CB_{1}^{2}}=\frac{3}{2}$.
∴$B_{1}(-\frac{\sqrt{3}}{2},\frac{3}{2})$.

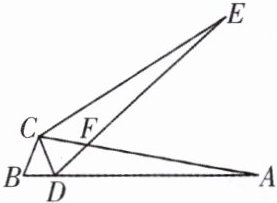
9. 如图，在△ABC中，点D在AB边上，CB = CD，将边CA绕点C旋转到CE的位置，使得∠ECA = ∠DCB，连接DE与AC交于点F，且∠B = 70°，∠A = 10°.
(1)求证：AB = ED.
(2)求∠AFE的度数.

答案：
(1)证明：
∵∠ECA = ∠DCB，
∴∠ECA + ∠ACD = ∠DCB + ∠ACD，即∠ECD = ∠BCA. 由旋转可得 CA = CE. 在△BCA 和△DCE 中，$\begin{cases}CB = CD,\\\angle BCA=\angle DCE,\\AC = EC.\end{cases}$
∴△BCA≌△DCE(SAS).
∴AB = ED.
(2)解：由
(1)中结论可得∠CDE = ∠B = 70°，又
∵CB = CD，
∴∠B = ∠CDB = 70°.
∴∠EDA = 180° - ∠BDE = 180° - 70°×2 = 40°.
∴∠AFE = ∠EDA + ∠A = 40° + 10° = 50°.

10. 如图是用围棋摆出的图案(把棋子的位置用有序数对表示，如A点在(5,1))，如果再摆一黑一白两枚棋子，使9枚棋子组成的图案既是轴对称图形又是中心对称图形，则下列摆放正确的是 （ ）

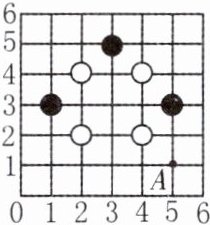
A. 黑(3,3)，白(3,1)
B. 黑(3,1)，白(3,3)
C. 黑(1,5)，白(5,5)
D. 黑(3,2)，白(3,3)

答案： B

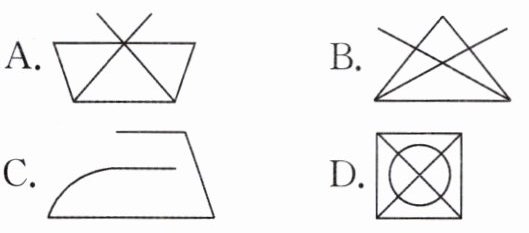
11. 如图，这四个图案都是某种衣物的洗涤说明，请指出不是利用图形的平移、旋转或轴对称设计的是 （ ）

答案： C

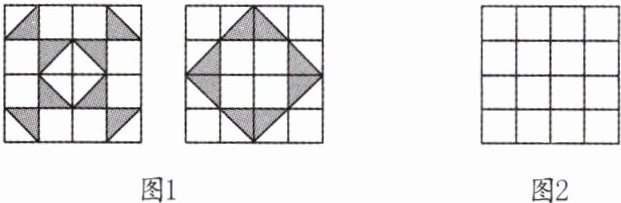
12. 认真观察图1的两个图中阴影部分构成的图案，回答下列问题：
(1)这两个图案都既是中心对称图形又是____________图形.
(2)请在图2中设计出你心中最美丽的图案，使它也具备上述两个特征.

答案：
解：
(1)轴对称
(2)所设计图案如图所示.