《2025年一线调研学业测评八年级数学下册北师大版》

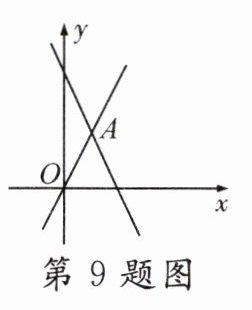
9. 如图，函数$y = 2x$和$y = ax + 4$的图象交于点$A(m,2)$，则不等式组$0\leqslant ax + 4\leqslant2x$的解集为（ ）

A. $x\geqslant1$
B. $x\geqslant2$
C. $1\leqslant x\leqslant2$
D. $x\leqslant1$

答案： C【解析】$\because$点$A(m,2)$在函数$y = 2x$的图象上，$\therefore2 = 2m$。解得$m = 1$。$\therefore A(1,2)$。把点$A(1,2)$代入$y=ax + 4$，得$2=a + 4$。解得$a=-2$。$\therefore y=-2x + 4$。把$y = 0$代入$y=-2x + 4$，得$x = 2$。$\therefore y=-2x + 4$与$x$轴的交点坐标为$(2,0)$。由函数图象可知，当$x\geqslant1$时，$ax + 4\leqslant2x$；当$x\leqslant2$时，$ax + 4\geqslant0$。$\therefore$不等式组$0\leqslant ax + 4\leqslant2x$的解集为$1\leqslant x\leqslant2$。

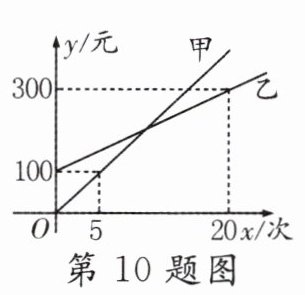
10. 某生态体验园推出了甲、乙两种消费卡. 甲、乙两卡所需费用$y_{甲}$，$y_{乙}$（单位：元）与入园次数$x$（单位：次）的函数关系如图所示. 当$x$满足__________时，$y_{甲}＞y_{乙}$.

答案： $x＞10$

11. 某商店销售A，B两种商品，每件的售价分别为$20$元、$30$元. “五一”期间，该商店决定对这两种商品进行促销活动，活动方案如图所示.
优惠方案一：
购买A商品超过$15$件后，超出部分五折，否则不打折.
购买B商品一律九折.
优惠方案二：
两种商品无论购买多少，一律八折.
若小红打算到该商店购买$m$件A商品和$20$件B商品，根据以上信息，请回答下列问题.
（1）分别用含$m$的代数式表示按照方案一和方案二所需的费用$w_{1}$和$w_{2}$.
（2）就$m$的不同取值，说明选择哪种方案购买更合算.（两种优惠方案不能同时享受）

答案： 解：
(1)当$0\leqslant m\leqslant15$时，$w_1=20m + 30\times0.9\times20=20m + 540$；当$m＞15$时，$w_1=20\times15+20\times0.5(m - 15)+30\times0.9\times20=10m + 690$。
综上，可知$w_1=\begin{cases}20m + 540(0\leqslant m\leqslant15)\\10m + 690(m＞15)\end{cases}$。
$w_2=(20m + 30\times20)\times0.8=16m + 480$。
(2)若$0\leqslant m\leqslant15$，则$20m + 540＞16m + 480$，故选择方案二购买更合算。
若$m＞15$，
$\because10m + 690＞16m + 480$时，$m＜35$，
$\therefore$当$15＜m＜35$时，选择方案二购买更合算。
综上所述，当$0\leqslant m＜35$时，选择方案二购买更合算；当$m = 35$时，两种方案费用一样；当$m＞35$时，选择方案一购买更合算。