《2025年一线调研学业测评八年级数学下册北师大版》

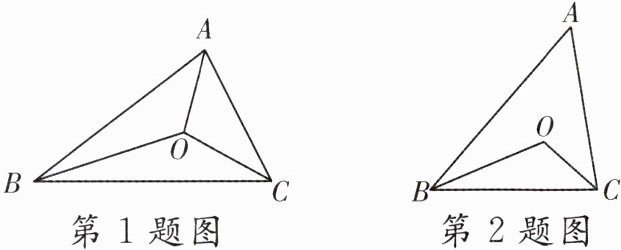
1. 如图所示，BO与CO分别是△ABC的∠ABC和∠ACB的平分线，若∠BAO = 30°，则∠CAB的度数为（ ）

A. 50°
B. 55°
C. 60°
D. 不能确定

答案： C

2. 如图，在△ABC中，BO，CO分别是∠ABC，∠ACB的平分线，∠A = 50°，则∠BOC的度数为（ ）
A. 115°
B. 120°
C. 125°
D. 130°

答案： A

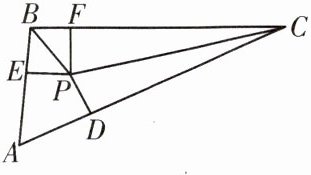
3. 如图，在△ABC中，PD⊥AC，PE⊥AB，PF⊥BC，PD = PE = PF，求证：∠BPC = 90° + $\frac{1}{2}$∠BAC.

答案： 证明：
∵$PD\perp AC$，$PE\perp AB$，$PF\perp BC$，$PD = PE = PF$，
∴点$P$是$\triangle ABC$三个内角平分线的交点.
∴$CP$平分$\angle ACB$，$BP$平分$\angle ABC$.
∴$\angle PCB=\frac{1}{2}\angle ACB$，$\angle PBC=\frac{1}{2}\angle ABC$.
∴$\angle BPC = 180^{\circ}-\angle PCB-\angle PBC = 180^{\circ}-\frac{1}{2}(\angle ACB+\angle ABC)=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle BAC)=90^{\circ}+\frac{1}{2}\angle BAC$.

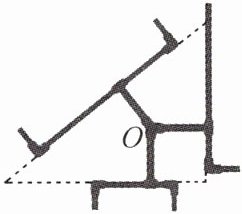
4. 如图，是某油路管道的一部分，延伸其中三条支路恰好构成一个直角三角形，其三边长分别为6m，8m，10m，输油中心O在到三条支路距离相等的地方，则中心O到三条支路的管道总长（计算时视管道为线，中心O为点）为（ ）

A. 24m
B. 12m
C. 10m
D. 6m

答案： D

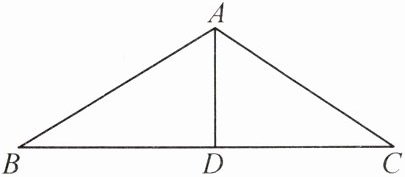
5. 已知：如图，在△ABC中，D是BC上一点，连接AD，在△ABC的内部是否存在到∠C的两边距离相等的点？在△ABC的内部是否存在一点E，使得该点既到∠B的两边距离相等，又到∠DAC的两边距离相等？（不写作法，保留作图痕迹）

答案：
解：存在. 如图，该点在$\angle ACB$的平分线$CF$上.
存在，点$E$为$\angle ABC$的平分线与$\angle DAC$的平分线的交点，如图，点$E$即为所求.

6. 如图，△ABC的三边AB，BC，CA的长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则$S_{\triangle ABO}:S_{\triangle BCO}:S_{\triangle CAO}$等于（ ）

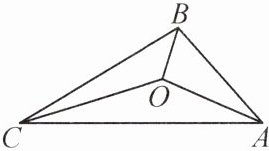
A. 1:1:1
B. 1:2:3
C. 2:3:4
D. 3:4:5

答案： C