《2025年一线调研学业测评八年级数学下册北师大版》

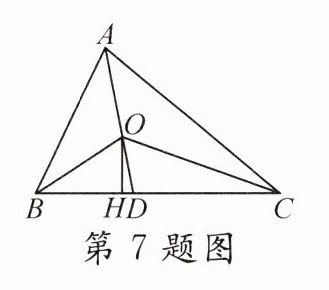
7. 如图，已知△ABC，∠ABC，∠ACB的平分线交于点O，连接AO并延长交BC于点D，OH⊥BC于点H，若∠BAC = 60°，OH = 3cm，则OA的长为（ ）

A. 6cm
B. 5cm
C. 4cm
D. 3cm

答案： A

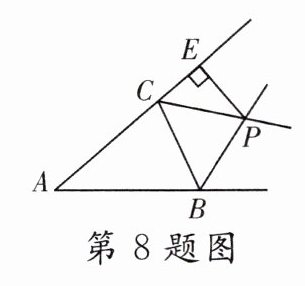
8. 如图，△ABC的两条外角平分线BP，CP相交于点P，PE⊥AC交AC的延长线于点E. 若△ABC的周长为11，PE = 2，$S_{\triangle BPC}=2$，则$S_{\triangle ABC}$ = （ ）

A. 10
B. 9
C. 8
D. 7

答案： D

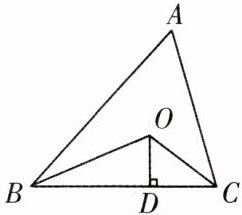
9. 如图，已知△ABC的周长是18，∠ABC和∠ACB的平分线交于点O，OD⊥BC于点D，若OD = 3，求△ABC的面积.

答案：
解：过$O$点作$OE\perp AB$于点$E$，$OF\perp AC$于点$F$，连接$OA$.
∵$OB$平分$\angle ABC$，$OD\perp BC$，$OE\perp AB$，$OF\perp AC$，
∴$OE = OF = OD = 3$.
∴$S_{\triangle ABC}=S_{\triangle OAB}+S_{\triangle OBC}+S_{\triangle OAC}=\frac{1}{2}OE\cdot AB+\frac{1}{2}OD\cdot BC+\frac{1}{2}OF\cdot AC=\frac{1}{2}OD\cdot(AB + BC + AC)=\frac{3}{2}\times18 = 27$.

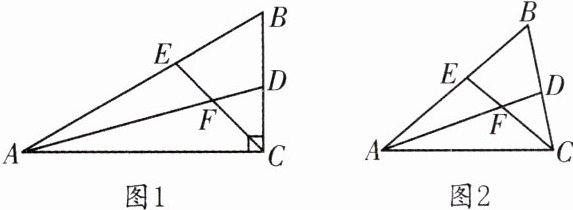
10. 如图1，在Rt△ABC中，∠ACB = 90°，∠B = 60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F.
（1）请判断FE与FD之间的数量关系，并说明理由.
（2）如图2，如果∠ACB不是直角，其他条件不变，（1）中所得结论是否仍然成立？请说明理由.

答案：
解：
(1)$FE = FD$. 理由如下：
如图 1，过点$F$作$FM\perp AB$于点$M$，$FN\perp BC$于点$N$，则$\angle FME=\angle FND = 90^{\circ}$，
∵$AD$，$CE$分别是$\angle BAC$，$\angle BCA$的平分线，$\angle ACB = 90^{\circ}$，$\angle B = 60^{\circ}$，
∴$\angle BAD=\frac{1}{2}\angle BAC = 15^{\circ}$.
∴$\angle FEM=\angle BAC+\angle ACE = 30^{\circ}+45^{\circ}=75^{\circ}$，$\angle FDN=\angle B+\angle BAD = 60^{\circ}+15^{\circ}=75^{\circ}$.
∴$\angle FEM=\angle FDN$.
∵$\angle BAC$，$\angle BCA$的平分线$AD$，$CE$交于点$F$，
∴点$F$在$\angle ABC$的平分线上. 又
∵$FM\perp AB$，$FN\perp BC$，
∴$FM = FN$.
∴$\triangle FEM\cong\triangle FDN(AAS)$.
∴$FE = FD$.

(2)成立. 理由如下：
如图 2，过点$F$作$FM\perp AB$于点$M$，$FN\perp BC$于点$N$，则$FM = FN$，$\angle FME=\angle FND = 90^{\circ}$.
∵$\angle FDN=\angle B+\angle BAD = 60^{\circ}+\frac{1}{2}\angle BAC$，$\angle FEM=\angle BAC+\angle ACE=\angle BAC+\frac{1}{2}(180^{\circ}-\angle B-\angle BAC)=\angle BAC+\frac{1}{2}(180^{\circ}-60^{\circ}-\angle BAC)=60^{\circ}+\frac{1}{2}\angle BAC$，
∴$\angle FEM=\angle FDN$.
∴$\triangle FEM\cong\triangle FDN(AAS)$.
∴$FE = FD$.