第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. 如图,在△ABC中,∠ACB = 90°,BC = 16cm,以点A为圆心、AC长为半径画弧,交线段AB于点D;以点B为圆心、BD长为半径画弧,交线段BC于点E. 若BD = CE,则AC的长为( )
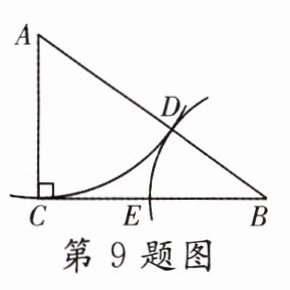
A. 12cm
B. 13cm
C. 14cm
D. 15cm

A. 12cm
B. 13cm
C. 14cm
D. 15cm
答案:
A
10. 如图,已知圆柱的底面直径BC = $\frac{6}{\pi}$cm,高AB = 3cm,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为________cm.
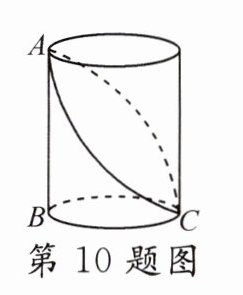

答案:
6$\sqrt{2}$
11. 易错题 已知CD是△ABC的边AB上的高,若CD = $\sqrt{3}$,AD = 1,AB = 2AC,则BC的长为______________.
答案:
2$\sqrt{3}$或2$\sqrt{7}$ [解析]分两种情况:①当∠BAC是锐角时,如图1;②当∠BAC是钝角时,如图2.分别根据勾股定理计算即可.


2$\sqrt{3}$或2$\sqrt{7}$ [解析]分两种情况:①当∠BAC是锐角时,如图1;②当∠BAC是钝角时,如图2.分别根据勾股定理计算即可.


12. 已知命题“直角三角形斜边上的中线等于斜边的一半”.
(1)写出逆命题:______________________________.
(2)逆命题是真命题还是假命题?如果是真命题,请画出“图形”,写出“已知”,“求证”,再进行“证明”;如果是假命题,请举反例说明.
(1)写出逆命题:______________________________.
(2)逆命题是真命题还是假命题?如果是真命题,请画出“图形”,写出“已知”,“求证”,再进行“证明”;如果是假命题,请举反例说明.
答案:
解:
(1)如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形,且这条边为斜边
(2)是真命题.
已知:如图,△ABC中,BD是AC边上的中线,BD = $\frac{1}{2}AC$,
求证:∠ABC = 90°
 证明:
证明:
∵BD是AC边上的中线,且BD = $\frac{1}{2}AC$,
∴AD = CD = BD = $\frac{1}{2}AC$.
∴∠A = ∠ABD,∠C = ∠CBD.
∴∠A + ∠C = ∠ABD + ∠CBD,即∠A + ∠C = ∠ABC. 又
∵∠A + ∠C + ∠ABC = 180°,
∴∠ABC = 90°.
解:
(1)如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形,且这条边为斜边
(2)是真命题.
已知:如图,△ABC中,BD是AC边上的中线,BD = $\frac{1}{2}AC$,
求证:∠ABC = 90°
 证明:
证明:∵BD是AC边上的中线,且BD = $\frac{1}{2}AC$,
∴AD = CD = BD = $\frac{1}{2}AC$.
∴∠A = ∠ABD,∠C = ∠CBD.
∴∠A + ∠C = ∠ABD + ∠CBD,即∠A + ∠C = ∠ABC. 又
∵∠A + ∠C + ∠ABC = 180°,
∴∠ABC = 90°.
13. 如图,在△ABC中,∠A = 30°,∠B = 60°,CE平分∠ACB.
(1)∠ACE的度数为______.
(2)若CD⊥AB于点D,∠CDF = 75°,求证:△CFD是直角三角形.
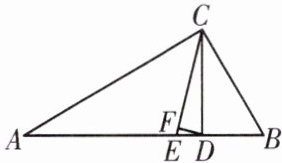
(1)∠ACE的度数为______.
(2)若CD⊥AB于点D,∠CDF = 75°,求证:△CFD是直角三角形.

答案:
(1)解:45° 提示:在△ABC中,∠A=30°,∠B=60°,
∴∠ACB=180°−30°−60°=90°.又
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=45°.
(2)证明:
∵CD⊥AB,∠B=60°,
∴∠BCD=90°−60°=30°,又
∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE−∠BCD=15°.又
∵∠CDF=75°,
∴∠CFD=180°−75°−15°=90°,
∴△CFD是直角三角形.
(1)解:45° 提示:在△ABC中,∠A=30°,∠B=60°,
∴∠ACB=180°−30°−60°=90°.又
∵CE平分∠ACB,
∴∠ACE=$\frac{1}{2}$∠ACB=45°.
(2)证明:
∵CD⊥AB,∠B=60°,
∴∠BCD=90°−60°=30°,又
∵∠BCE=∠ACE=45°,
∴∠DCF=∠BCE−∠BCD=15°.又
∵∠CDF=75°,
∴∠CFD=180°−75°−15°=90°,
∴△CFD是直角三角形.
14. 如图,台风中心沿东西方向由A向B移动,AB = 1000km,已知点C为一海港,且点C与直线AB上的两点A,B的距离分别为AC = 600km,BC = 800km,以台风中心为圆心,周围500km以内为受影响区域.
(1)∠ACB的度数为______.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28km/h,则台风影响该海港持续的时间有______h.
(1)∠ACB的度数为______.
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28km/h,则台风影响该海港持续的时间有______h.

答案:
解:
(1)90°
(2)海港C受台风影响.理由:过点C作CD⊥AB,
∵△ABC是直角三角形,
∴S_{△ABC} = $\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB$.
∴CD = 480km.
∵480km<500km,
∴海港C受台风影响.
(3)10
(1)90°
(2)海港C受台风影响.理由:过点C作CD⊥AB,
∵△ABC是直角三角形,
∴S_{△ABC} = $\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB$.
∴CD = 480km.
∵480km<500km,
∴海港C受台风影响.
(3)10
查看更多完整答案,请扫码查看


