《2024年新课程课堂同步练习册九年级数学上册人教版》

2. 如图3,在△ABC中,AC= BC= 5 cm,∠ACB= 120°,求△ABC的外接圆的半径.

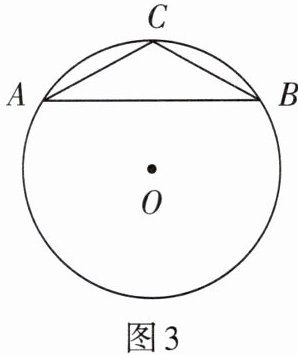
答案： 解：连接OA，OB，OC，
∵$AC=BC=5\ \mathrm {cm}$
∴$\widehat{AC}=\widehat{BC}$
∴∠AOC=∠BOC
∵∠ACB=120°
∴∠AOC=∠BOC=60°
∵OA=OC
∴△AOC为等边三角形
∴$OA=AC=5\ \mathrm {cm}，$即△ABC的外接圆的半径为$5\ \mathrm {cm}$

3. 建立平面直角坐标系,作以原点O为圆心,半径为4的⊙O,试确定点A(-2,-3),B(4,-2),C(-2√3,2)与⊙O的位置关系.

答案： 解：$OA=\sqrt {{(-2)}^2+{(-3)}^2}=\sqrt {13}＜4，$
$ OB=\sqrt {{4}^2+{(-2)}^2}=2\sqrt {5}＞4，$
$ OC=\sqrt {{(-2\sqrt {3})}^2+{2}^2}=4$
∵OA＜4，OB＞4，OC=4
∴点A在⊙O内，点B在⊙O外，点C在⊙O上

1. 直线l与半径为r的⊙O相交,且点O到直线l的距离为5,则r的取值范围是( )

A.r= 5
B.r＞5
C.r＜5
D.r≤5

答案： B

2. 点A为直线l上任一点,过点A与直线l相切的圆有( )

A.1个
B.2个
C.不存在
D.无数个

答案： D