《2024年新课程课堂同步练习册九年级数学上册人教版》

2. 某商场以每件50元的价格购进一种商品,销售中发现这种商品每天的销售数量m(单位:件)与每件的销售价格x(单位:元)满足一次函数关系,其图象如图1所示.
(1)每天销售数量m(单位:件)与每件销售价格x(单位:元)的函数解析式是______;
(2)求该商场每天销售这种商品的销售利润y(单位:元)与每件的销售价格x(单位:元)之间的函数解析式;
(3)在保证盈利的条件下,每件商品的销售价格在什么范围内,每天的销售利润随着销售价格的提高而增加?

答案： $m=-x+100(0\leqslant x\leqslant 100)$
解：
(2)每件商品的利润为x-50，所以每天的利润
y=(x-50)(-x+100)
∴函数解析式为$y=-{x}^2+150x-5000$
(3)
∵$x=-\frac {150}{2×(-1)}=75$
∴在50＜x＜75元时，每天的销售利润随着x的增大而增大

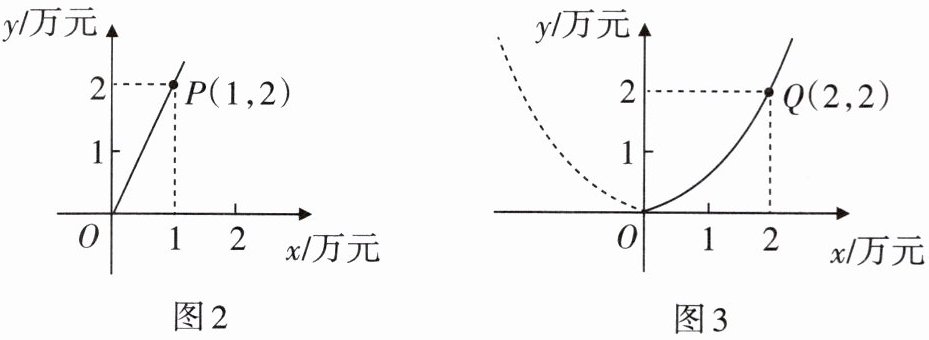
3. 某市近几年城市建设快速发展,对花木的需求量逐年增加. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润$y_{1}$与投资量x成正比例关系,如图2所示;种植花卉的利润$y_{2}$与投资量x成二次函数关系,如图3所示.
(1)分别求出利润$y_{1}与y_{2}$关于投资量x的函数解析式.
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润? 他能获取的最大利润是多少?

答案： 解：$(1)y_1=2x，$$y_2=\frac 1 2{x}^{2}$
(2)设x万元投资花卉，则(8-x)万元投资树木，设获得的利润为y万元．
由题意得，$y=\frac 1 2{x}^{2}+2(8-x)=\frac 1 2{x}^{2}-2x+16=\frac 1 2{(x-2)}^{2}+14$
当x=2时，y_{最小}=14；
当x=8时，y_{最大}=32．
∴他至少获得14万元利润，能获取的最大利润是32万元．