《2024年新课程课堂同步练习册九年级数学上册人教版》

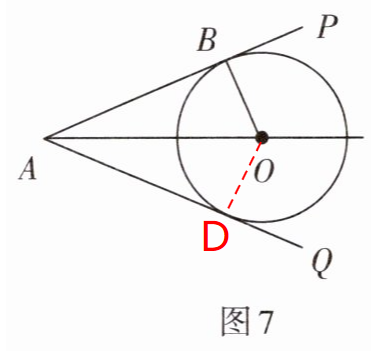
1. 如图7,O为∠PAQ的平分线上的一点,OB⊥AP于点B,以O为圆心,OB为半径作⊙O. 求证：AQ与⊙O相切.

答案：
证明：过点O作OD⊥AQ{于} 点D，
∵AO平分∠PAQ，OB⊥AP，OD⊥AQ
∴OB=OD，即点O到AQ的距离等于半径
∴AQ 与⊙O相切

2. 如图8,PA,PB是⊙O的切线,A,B分别为切点,∠OAB= 30°.
(1)求∠APB的度数；
(2)当OA= 3时,求AP的长.

答案： 解：
(1)
∵OA=OB，∠OAB=30°
∴∠OBA=∠OAB=30°
∴∠AOB=120°
∵PA，PB是⊙O的切线
∴∠OAP=∠OBP=90°
∴∠APB=360°-90°-90°-120°=60°
(2)连接OP，
∵PA，PB是⊙O的切线
∴PO平分∠APB
∴$∠APO=\frac 1 2∠APB=30°$
∵∠OAP=90°
∴$AP=\sqrt {3}OA=3\sqrt {3}$

3. 如图9,AB为⊙O的直径,AC平分∠DAB交⊙O于点C,DC⊥AD于D.
求证：DC是⊙O的切线.

答案： 证明：连接OC，
∵AC平分∠DAB
∴∠CAD=∠CAB
∵OA=OC
∴∠CAB=∠ACO
∴∠CAD=∠ACO
∴AD//OC
∵AD⊥DC
∴OC⊥DC
∴DC是⊙O的切线