《2024年新课程课堂同步练习册九年级数学上册人教版》

3. 如图8,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线$ x= -\frac{1}{2} $.
(1)求抛物线的解析式；
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.

答案： 解：
(1)设抛物线的解析式为$y=a{(x+\frac 1 2)}^{2}+k$
把A(2，0)，C(0，3)代入得
$ {{\begin{cases} {{\frac {25}4a+k=0}} \\ {\frac 1 4a+k=3} \end{cases}}}$
解得${{\begin{cases} {{a=-\frac 1 2}} \\ {k=\frac {25}8} \end{cases}}}$
∴抛物线的解析式为$y=-\frac 1 2{(x+\frac 1 2)}^{2}+\frac {25}8$
即$y=-\frac 1 2{x}^{2}-\frac1 2x+3$
(2)由y=0得$-\frac 12{(x+\frac 1 2)}^{2}+\frac {25}8=0$
∴$x_1=2，$$x_2=-3$
∴B(-3，0)
①CM=BM时，
∵BO=CO=3，即△BOC是等腰直角三角形
∴当M点在原点O时，△MBC是等腰三角形
∴M点坐标为(0，0)
②BC=BM时，在Rt△BOC中，BO=CO=3，由勾股定理得$BC=\sqrt {{OC}^{2}+{OB}^{2}}$
∴$BC=3\sqrt {2}$
∴$BM=3\sqrt {2}$
∴M点坐标为$(3\sqrt {2}-3，$0)

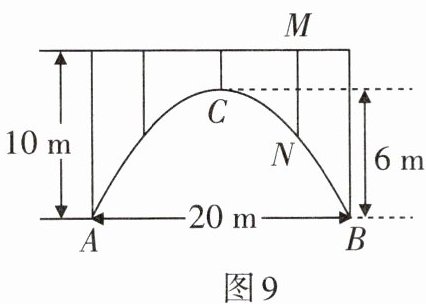
4. 一座拱桥的轮廓是抛物线(如图9所示),拱高6 m,跨度20 m,相邻两支柱间的距离均为5 m.
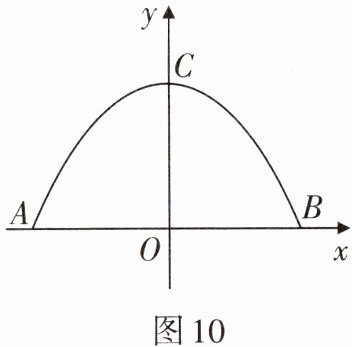
(1)将抛物线放在所给的直角坐标系中(如图10所示),其关系式为$ y= ax^2+c $的形式,请根据所给的数据求出a,c的值；
(2)求支柱MN的长度；
(3)拱桥下地面是双向行车道(正中间是一条宽2 m的隔离带),其中的一条行车道能否并排行驶宽2 m,高3 m的三辆汽车(汽车间的间隔忽略不计)？请说说你的理由.

答案： 解：
(1)将B(10，0)和C(0，6)代入，得
$ {{\begin{cases} {{100a+c=0}} \\ {c=6} \end{cases}}}$
解得，${{\begin{cases} {{a=-\frac 3 {50}}} \\ {c=6} \end{cases}}}$
(2)当x=5时，$y=-\frac 3 {50}×{5}^{2}+6=\frac 9 2$
∴$MN=10-\frac 9 2=\frac {11}2m$
(3)当x=7时，$y=-\frac 3 {50}×{7}^{2}+6=\frac {153}{50}$
∵$\frac {153}{50}＞3$
∴能