第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
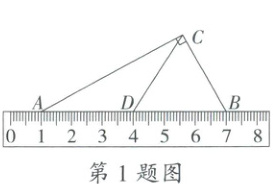
1.(3分)如图,将直角三角尺放置在刻度尺上,斜边上三个点$A$、$D$、$B$对应的刻度分别为1、4、7(单位:cm),则$CD$的长度为(
A.6
B.4.5
C.3.5
D.3
D
)A.6
B.4.5
C.3.5
D.3

答案:
1.D
2.(3分)如图是某商场一楼与二楼之间的手扶电梯示意图。其中$AB$,$CD$分别表示一楼、二楼地面的水平线,$\angle ABC = 150°$,$BC$的长是8 m,则乘电梯从点$B$到点$C$上升的高度$h$是(
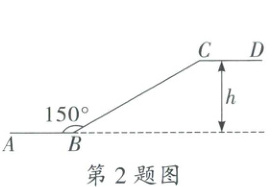
A.3 m
B.4 m
C.4.5 m
D.5 m
B
)
A.3 m
B.4 m
C.4.5 m
D.5 m
答案:
2.B
3.(3分)如图,在等边三角形$ABC$中,$AD$为$\angle BAC$的平分线,在$AB$,$CB$上分别取点$M$,$N$。且$AM = BN = 4$,$DN = 2$,在$AD$上有一动点$P$,则$PM + PN$的最小值为(
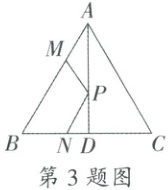
A.7
B.8
C.10
D.12
B
)
A.7
B.8
C.10
D.12
答案:
3.B 【解析】
∵BN = 4,DN = 2,
∴BD = 6.
∵等边三角
形ABC中,AD为∠BAC的平分线,
∴AD为等边三
角形的中线.AD所在的直线为△ABC的对称轴.
∴CD = BD = 6.
∴BC = 12.作点M关于AD的对称
点M',则点M'在线段AC上.
∴MP = M'P.
∵AM =
4,
∴AM' = AM = 4.
∵△ABC是等边三角形,
∴AC =
BC = 12,∠C = 60°.
∴CM' = 8.连接M'N交AD于点
P,
∴PM + PN = PM' + PN = M'N.
∵CN = CD + DN = 8,
∴CN = CM'.
∴△CNM'是等边三角形.
∴M'N = 8.
∴PM + PN的最小值为8.故选B.
∵BN = 4,DN = 2,
∴BD = 6.
∵等边三角
形ABC中,AD为∠BAC的平分线,
∴AD为等边三
角形的中线.AD所在的直线为△ABC的对称轴.
∴CD = BD = 6.
∴BC = 12.作点M关于AD的对称
点M',则点M'在线段AC上.
∴MP = M'P.
∵AM =
4,
∴AM' = AM = 4.
∵△ABC是等边三角形,
∴AC =
BC = 12,∠C = 60°.
∴CM' = 8.连接M'N交AD于点
P,
∴PM + PN = PM' + PN = M'N.
∵CN = CD + DN = 8,
∴CN = CM'.
∴△CNM'是等边三角形.
∴M'N = 8.
∴PM + PN的最小值为8.故选B.
4.(3分)如图,在$\triangle ABC$中,$AB = BC = 12$,$D$为$AB$的中点,$ED\perp AB$,垂足为点$D$,交$BC$于点$E$,若$\triangle AEC$的周长为22,则$AC = $

10
。
答案:
4.10 【解析】
∵D为AB的中点,ED⊥AB,
∴AE =
BE.
∵△AEC的周长为22,
∴AC + CE + AE = AC + CE
+ BE = AC + BC = 22.
∵BC = 12,
∴AC = 10.
∵D为AB的中点,ED⊥AB,
∴AE =
BE.
∵△AEC的周长为22,
∴AC + CE + AE = AC + CE
+ BE = AC + BC = 22.
∵BC = 12,
∴AC = 10.
5.(3分)如图,在$\triangle ABC$中,$\angle ACB = 90°$,$\angle A = 30°$,$BC = 4$,以点$C$为圆心,$CB$长为半径作弧,交$AB$于点$D$;再分别以点$B$和点$D$为圆心,大于$\frac{1}{2}BD$的长为半径作弧,两弧相交于点$E$,作射线$CE$交$AB$于点$F$,则$AF$的长为
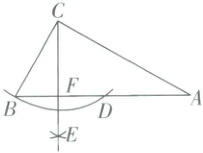
]
6
。
]
答案:
5.6 【解析】连接CD.
∵在△ABC中,∠ACB = 90°,
∠A = 30°,BC = 4,
∴∠ABC = 60°,AB = 2BC = 8.由
题可知BC = CD = 4,CE是线段BD的垂直平分线,
∴△BCD是等边三角形,
∴BD = BC = 4,$BF = \frac{1}{2}BD$
= 2,
∴AF = AB - BF = 6.
∵在△ABC中,∠ACB = 90°,
∠A = 30°,BC = 4,
∴∠ABC = 60°,AB = 2BC = 8.由
题可知BC = CD = 4,CE是线段BD的垂直平分线,
∴△BCD是等边三角形,
∴BD = BC = 4,$BF = \frac{1}{2}BD$
= 2,
∴AF = AB - BF = 6.
6.(10分)如图,在$\triangle ABC$中,$AD$是$\angle BAC$的平分线,$AD$的垂直平分线交$AB$于点$E$,交$CB$的延长线于点$F$,连接$DE$,$AF$。
(1)判断$DE$与$AC$的位置关系,并说明理由;
(2)求证:$\angle C = \angle EAF$。
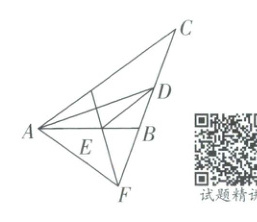
(1)判断$DE$与$AC$的位置关系,并说明理由;
(2)求证:$\angle C = \angle EAF$。

答案:
6.
(1)解:DE//AC,理由:
∵AD是∠BAC的平分线,
∴
∠CAD = ∠BAD.
∵EF垂直平分AD,
∴AE = DE,
∴∠BAD = ∠EDA,
∴∠CAD = ∠EDA,
∴DE//AC;
(2)证明:
∵EF垂直平分AD,
∴EA = ED,FA = FD,
∴∠EAD = ∠EDA,∠FAD = ∠FDA,
∴∠EAF =
∠EDF.
∵DE//AC,
∴∠C = ∠EDF,
∴∠C
= ∠EAF.
(1)解:DE//AC,理由:
∵AD是∠BAC的平分线,
∴
∠CAD = ∠BAD.
∵EF垂直平分AD,
∴AE = DE,
∴∠BAD = ∠EDA,
∴∠CAD = ∠EDA,
∴DE//AC;
(2)证明:
∵EF垂直平分AD,
∴EA = ED,FA = FD,
∴∠EAD = ∠EDA,∠FAD = ∠FDA,
∴∠EAF =
∠EDF.
∵DE//AC,
∴∠C = ∠EDF,
∴∠C
= ∠EAF.
查看更多完整答案,请扫码查看


