《2025年追梦之旅初中期末真题篇八年级数学上册人教版河南专版》

6.某数学兴趣小组的同学打算测量一个小口圆形容器内径时遇到了困难,小组同学们借用学习过的三角形全等的知识合作制作了特制工具测量器.如图所示,将等长的钢条 AD 和 BC 的中点 O 焊接在一起,制作了一把“X 形卡钳”.根据“X 形卡钳”的制作原理能判断△ABO≌△DCO,从而测量出 AB 的长就等于内径 CD 的长.请写出△ABO≌△DCO的理由:SAS.

答案： 6.SAS

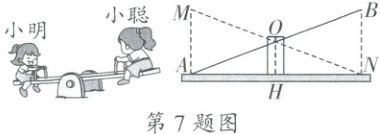
7.如图,小聪和小明玩跷跷板游戏,支点 O 是跷跷板的中点(即 OA=OB),支柱 OH 垂直于地面,两人分别坐在跷跷板 A,B 两端，当 A 端落地时,$∠AOH=70°$,则 AB 上下可转动的最大角度$∠AOM=$$40^{\circ}$.

答案： 7.$40^{\circ}$　[解析]由题意得：$AM// OH$，$\therefore \angle AOH = \angle OAM = 70^{\circ}$.
$\because OM = OA$，$\therefore \angle M = \angle OAM = 70^{\circ}$，$\therefore \angle AOM = 180^{\circ} - \angle M - \angle OAM = 40^{\circ}$.

8.(9分)已知:如图1,直线 MN和直线 MN外一点 P.
求作:直线 PQ,使直线 PQ//MN.


(1)使用直尺和圆规,按照小智的作图思路补全图1(保留作图痕迹);
(2)完成下面的证明:
证明:∵AB 平分$∠PAN$,∴$∠PAB=∠NAB$.∵PA=PQ,∴$∠PAB=∠PQA$(等边对等角 ).
∴$∠NAB=∠PQA$.∴PQ//MN(内错角相等，两直线平行 ).
(3)参考小智的作图思路和流程,另外设计一种作法,利用直尺和圆规在图2中完成.(保留作图痕迹,不用写作法和证明)

答案：
8.解：
(1)如图，直线$PQ$即为所求；
　　　　　　
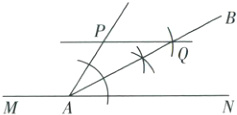
(2)等边对等角　内错角相等，两直线平行
(3)如图.直线$PQ$即为所求.