《2025年追梦之旅初中期末真题篇八年级数学上册人教版河南专版》

20. (9分)如图,在$\triangle ABC$中,$CD$是$AB$边上的中线,$E,F$为直线$CD$上的点,连接$AE,BF$,且$AE// BF$.
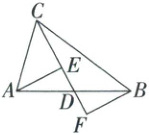
(1)求证:$\triangle ADE\cong\triangle BDF$;
(2)若$CF = 15$,$CE = 8$,求$DE$的长.

答案： 20.
(1)证明:
∵CD是AB边上的中线,
∴AD=BD,
∵AE//BF,
∴∠EAD=∠FBD,在△ADE和△BDF中,
$\begin{cases}∠EAD=∠FBD\\AD=BD\\∠ADE=∠BDF\end{cases}$
∴△ADE≌△BDF(ASA);
(2)解:
∵CF=15,CE=8,
∴EF=CF - CE=15 - 8=7,
∵△ADE≌△BDF,
∴DE=DF,
∴$DE=\frac{1}{2}×EF=\frac{1}{2}×7=3.5.$

21. (9分)2024年11月《中华人民共和国首届青少年三大球运动会》在长沙举行,某校为响应国家政策,课后延时服务开设了多个社团.“排球少年”社团需要添置一些排球,第一次购买花费$3000$元,因报名学生较多排球不够,第二次又花费$3000$元购买,但单价比原来上涨了$25\%$,结果第二次购买的排球比第一次少$15$个.
(1)求购进的两批排球单价;
(2)求该社团前后两次一共购买排球的数量.

答案： 21.解:
(1)设第一批购进的排球单价为x元,则第二批购进的排球单价为(1+25%)x元,由题意,得$\frac{3000}{x}-\frac{3000}{(1+25%)x}=15,$解得x=40,经检验,x=40是原分式方程的解.
∴第二批购进的排球单价为(1+25%)x=50,答:第一批购进的排球单价为40元,第二批购进的排球单价为50元;
(2)第一批购进的排球的数量为3000÷40=75(个),则第二批购进的排球数量为75 - 15=60(个),所以该社团前后两次一共购买排球的数量为75+60=135(个),答:该社团前后两次一共购买排球的数量为135个.