《2025年玩转母题八年级数学全一册人教版》

例 如图1，在△ABC所在平面内求作一点P，使它到三角形的三个顶点的距离之和最小。这个问题是有着“业余数学家之王”美誉的法国律师费马，在1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”。
(1) 解决这种问题的经典方法就是利用旋转，你可以利用所学知识说明理由吗？

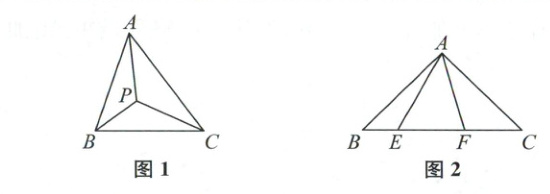
(2) 如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点，且∠EAF=45°，判断BE、EF、FC之间的数量关系，并说明理由。
1 信息提取
(1) 如图1，在△ABC所在平面内求作一点P，使它到三角形的三个顶点的距离之和最小。PA+PB+PC的值最小
(2) 如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点，且∠EAF=45°，判断BE、EF、FC之间的数量关系，并说明理由。∠EAF=21​∠CAB
2 思路精析
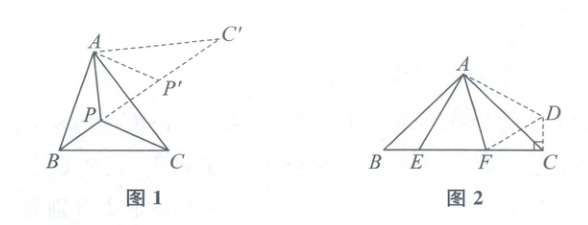
(1) 把△APC绕点A逆时针旋转60°，得到△AP'C'，连接PP'，把PA+PB+PC的最小值转化成BP+PP'+P'C'的最小值；
(2) 把△BAE绕点A逆时针旋转90°，得到△CAD，连接DF，利用旋转的性质得到CD=BE，再通过证明△FCD为直角三角形，得到DF²=CD²+FC²，最后证明△AFE≌△AFD，得到EF=DF，即可得出结论。
3 超详解答
解：(1) 如图1，把△APC绕点A逆时针旋转60°，得到△AP'C'，连接PP'，
由旋转可知∠PAP'=60°，AP=AP'，P'C'=PC。
∴△APP'为等边三角形。
∴AP=PP'。
∴PA+PB+PC=PP'+PB+P'C'。
∴当B、P、P'、C'四点在同一条直线上时，PA+PB+PC的值最小。

(2) EF²=BE²+FC²。理由如下：
∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°。
如图2，把△BAE绕点A逆时针旋转90°，得到△CAD，连接DF
则∠BAE=∠CAD，∠B=∠ACD=45°，AE=AD，BE=CD
∴∠DCF=∠ACB+∠ACD=90°。
∴DF²=CD²+FC²=BE²+FC²。
∵∠EAF=45°，
∴∠DAF=∠CAD+∠CAF=∠BAE+∠CAF=∠BAC−∠EAF=45°。
∴∠EAF=∠DAF=45°。
在△AFE和△AFD中，⎩⎨⎧​AE=AD,∠EAF=∠DAF,AF=AF,​
∴△AFE≌△AFD(SAS)。
∴EF=DF。
∴EF²=BE²+FC²。
学母题 找规律
当已知条件中出现有公共端点的两条相等的线段时，可以尝试利用旋转变换的方法将分散的线段或者角集中到一起。如费马点的证明将几条线段的和转化为“两点之间线段最短”的模型来解决。另外，还可以利用尺规作出本题中费马点的位置，感兴趣的同学可以试一试。

答案：
解：
(1) 如图1，把△APC绕点A逆时针旋转60°，得到△AP'C'，连接PP'，
由旋转可知∠PAP'=60°，AP=AP'，P'C'=PC。
∴△APP'为等边三角形。
∴AP=PP'。
∴PA+PB+PC=PP'+PB+P'C'。
∴当B、P、P'、C'四点在同一条直线上时，PA+PB+PC的值最小。

(2) EF²=BE²+FC²。理由如下：
∵AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°。
如图2，把△BAE绕点A逆时针旋转90°，得到△CAD，连接DF
则∠BAE=∠CAD，∠B=∠ACD=45°，AE=AD，BE=CD
∴∠DCF=∠ACB+∠ACD=90°。
∴DF²=CD²+FC²=BE²+FC²。
∵∠EAF=45°，
∴∠DAF=∠CAD+∠CAF=∠BAE+∠CAF=∠BAC−∠EAF=45°。
∴∠EAF=∠DAF=45°。
在△AFE和△AFD中，$\begin{cases}AE=AD,\\∠EAF=∠DAF,\\AF=AF,\end{cases}$
∴△AFE≌△AFD(SAS)。
∴EF=DF。
∴EF²=BE²+FC²。